Tìm đkxđ  giải giúp mình câu 19,21,23,24,18,10,13 với
giải giúp mình câu 19,21,23,24,18,10,13 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐIều kiện:`x^2-7x+8>=0`
`<=>x^2-2*x*7/2+49/4-17/4>=0`
`<=>(x-7/2)^2-17/4>=0`
`<=>(x-7/2)^2>=17/4`
`<=>|x-7/2|>=sqrt{17}/2`
`<=>` \(\left[ \begin{array}{l}x \ge \dfrac{7+\sqrt{17}}{2}\\x \le \dfrac{-\sqrt{17}+7}{2}\end{array} \right.\)
`pt<=>x^2-7x+sqrt{x^2-7x+8}-12=0`
`<=>x^2-7x+8+sqrt{x^2-7x+8}-20=0`
Đặt `a=sqrt{x^2-7x+8}(a>=0)`
`pt<=>a^2+a-20=0`
`<=>a=4(tm),a=-5(l)`
`<=>x^2-7x+8=16`
`<=>x^2-7x-8=0`
`a-b+c=0`
`=>x_1=-1(tm),x_2=8(tm)`
Vậy `S={-1,8}`

\(\sqrt{\dfrac{1}{x^2-2x+1}}=\sqrt{\dfrac{1}{\left(x-1\right)^2}}\)
ĐKXĐ: \(\left(x-1\right)^2\ne0\Leftrightarrow x\ne1\)
Vậy \(x\in R,x\ne1\) thì căn thức xác định

Biểu thức này không có GTLN vì nếu cho x > 1 và \(x\rightarrow1\Rightarrow\dfrac{1}{\sqrt{x}-1}\rightarrow\infty\).

câu 2
\(...=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{\left(2+\sqrt{5}\right)^2}=\left|2-\sqrt{5}\right|-\left|2+\sqrt{5}\right|=-4\)
câu 1
\(P=\left(\frac{\sqrt{x}}{3+\sqrt{x}}+\frac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\frac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\frac{1}{\sqrt{x}}\right)\)
\(=\left(\frac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\right):\left(\frac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\)
\(=\frac{3\sqrt{x}+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}:\frac{2\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\frac{3}{\left(3-\sqrt{x}\right)}.\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{2\sqrt{x}+4}=\frac{-3\sqrt{x}}{2\sqrt{x}+4}\)
\(P< -1\Leftrightarrow\frac{-3\sqrt{x}}{2\sqrt{x}+4}+1< 0\Leftrightarrow-\sqrt{x}+4< 0\Leftrightarrow\sqrt{x}>4\Leftrightarrow x>16\)

12:
a: ĐKXĐ: -2x+3>=0
=>x<=3/2
b: ĐKXĐ: x^2<>0
=>x<>0
c: ĐKXĐ: x+3>0
=>x>-3
d:ĐKXĐ: -5/x^2+6>=0
=>x^2+6<0
=>x thuộc rỗng
4.
a) Ta có: \(\sqrt{x}=3\)
\(\Leftrightarrow x=3^2=9\)
Vậy \(x=9\)
b) Ta có: \(\sqrt{x}=\sqrt{5}\)
\(\Leftrightarrow x=\sqrt{5}^2=5\)
Vậy \(x=5\)
c) Ta có: \(\sqrt{x}=0\)
\(\Leftrightarrow x=0^2=0\)
Vậy \(x=0\)
d) Ta có: \(\sqrt{x}=-2\)
\(\Leftrightarrow x=-2^2=4\)
Vậy \(x=4\)

a: \(P=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b: \(P-1=\dfrac{\sqrt{a}-1-\sqrt{a}}{\sqrt{a}}=\dfrac{-1}{\sqrt{a}}< 0\)

Làm thế này nhé
(2x-6)y+x-3=18
(2x-6)y+x-18-3=0
(2x-6)y+x-21=0
sau đó bạn rút gọn nhé, ta làm như sau
2(x-3)=0
=> 2x= 2 x 3
=> x=3 nhé
giúp mình llàm câu b với nhé đã k cho bạn rồi nha
b, y = \(\frac{23}{x+7}\)




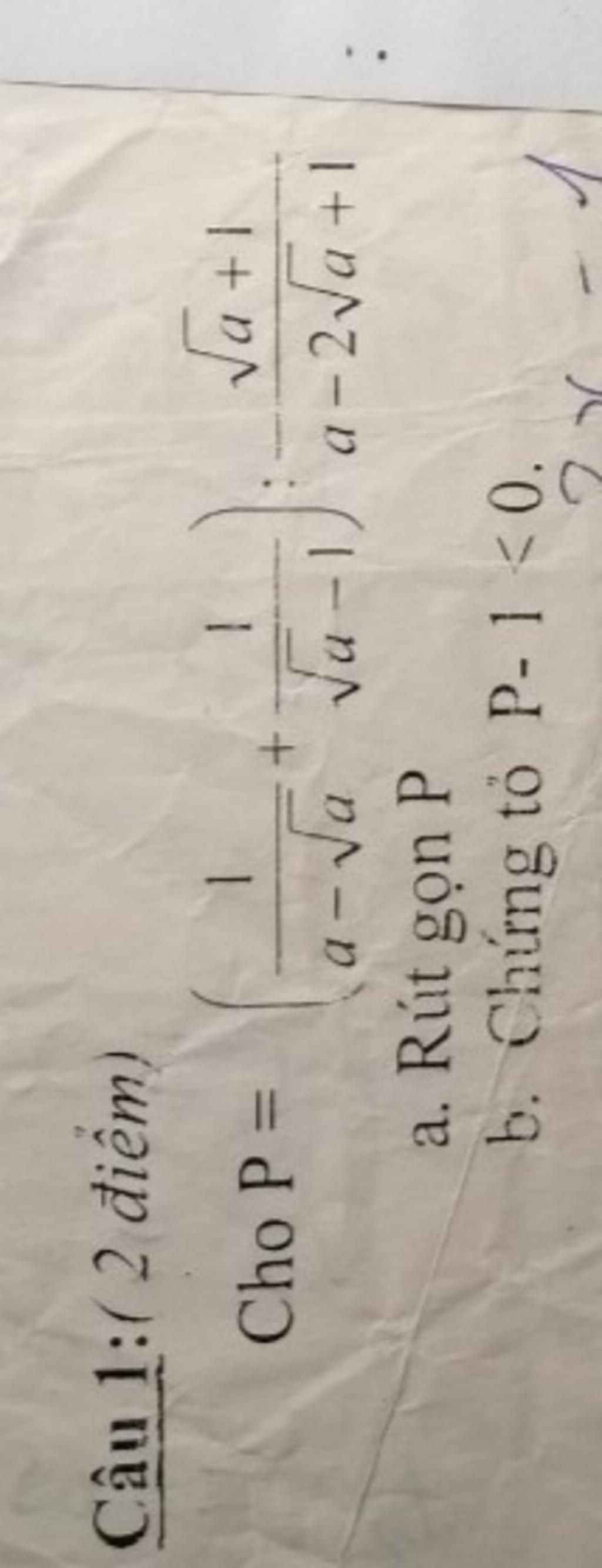
\(19,ĐKXĐ:\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}\ge0;x\ne5\\ \Leftrightarrow5-x< 0\left(-2\sqrt{6}+\sqrt{23}< 0\right)\\ \Leftrightarrow x>5\)
\(21,ĐKXĐ:x\ne7;\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}\ge0\\ \Leftrightarrow x-7>0\left(2\sqrt{15}-\sqrt{59}>0\right)\\ \Leftrightarrow x>7\)
\(23,ĐKXĐ:49x^2-24x+4\ge0\Leftrightarrow\left(49x^2-14\cdot\dfrac{12}{7}x+\dfrac{144}{49}\right)+\dfrac{52}{49}\ge0\\ \Leftrightarrow\left(7x-\dfrac{12}{7}\right)^2+\dfrac{52}{49}\ge0\\ \Leftrightarrow x\in R\)