Cho hai dao động điều hòa cùng phương x1=A1cos(ωt + π/3)cm và x2=A2cos(ωt - π/2)cm. Phương trình dao động tổng hợp là x = 5√3 cos(ωt + φ)cm. Khi A2 đạt giá trị lớn nhất thì A1 có giá trị là
HELP ME
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
A t 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ ⇔ 20 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos 11 18 π
⇒ 20 2 = A 1 + A 2 2 − 2 , 68. A 1 A 2 ≥ A 1 + A 2 2 − 2 , 68. A 1 + A 2 2 4 = 0 , 33 A 1 + A 2 2
⇒ A 1 + A 2 ≤ 34 , 9 c m .

Áp dụng công thức Freshnel về tổng hợp dao động ta có:
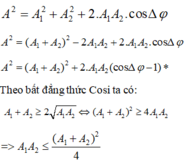
Thay vào biểu thức *, chú ý rằng biểu thức
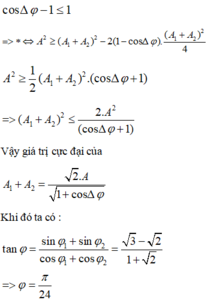
Đáp án C

Chọn A
![]()
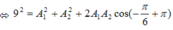
![]()
+ Coi phương trình (1) ẩn là A1 và A2 là tham số, ta có:
![]()
+ Để phương trình (1) có nghiệm ó Δ ≥ 0 => 0≤ A2 ≤ 18cm.
+ A2max = 18cm thay vào (1) => A1 = 9√3cm.
Áp dụng định lý hàm sin ta có:
\(\dfrac{5\sqrt{3}}{\dfrac{sin\pi}{3}}\) = \(\dfrac{Á_2}{sina}\) = \(\dfrac{A_3}{sinb}\)
⇒ A2 = \(\dfrac{5\sqrt{3}}{\dfrac{sin\pi}{3}}\)sina
Để A2 đạt giá trị lớn nhất, góc a bằng 90o, suy ra góc b bằng 60o
nên A1 = \(\dfrac{5\sqrt{3}}{\dfrac{sin\pi}{3}}\).sin60 = \(\dfrac{7,5}{\dfrac{sin\pi}{3}}\)