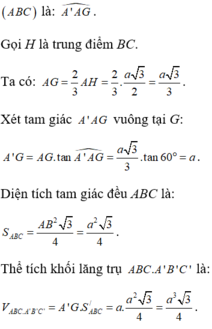Cho hinh lăng trụ đều ABC A'B'C' cạnh AA'= a khoảng cách từ AB' đến CC' là a că n3 diện tích tam giác ABC là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2021
Do \(AA'\text{/ / }CC'\Rightarrow AA'\) tạo với (ABC) một góc \(45^o\)
Mà \(A'H\text{⊥}\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(AA'\) và ( ABC)
\(\Rightarrow\widehat{A'AH=45^o\Rightarrow}\Delta A'AH\) vuông cân tại H
\(\Rightarrow A'H=AH=\dfrac{AB}{2}=\dfrac{a}{2}\)
\(^SABC=\dfrac{a^2\sqrt{3}}{4}=V=^SABC.^{A'H}=\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3.\sqrt{3}}{8}\)
CM
23 tháng 5 2019
Đáp án là B.
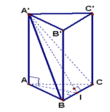
Gọi I là trung điểm BC.
Ta có Δ A B C đều nên A I = A B 3 2 = 2 3 .
A I ⊥ B C A A ' ⊥ B C ⇒ A ' I ⊥ B C
S A ' B C = 1 2 B C . A ' I ⇒ A ' I = 2 S A ' B C B C = 4
A A ' ⊥ ( A B C ) ⇒ A A ' ⊥ A I .
Xét Δ A ' A I vuông tại ⇒ A A ' = A ' I 2 − A I 2 = 2
Vậy V A B C . A ' B ' C ' = S A B C . A A ' = 4 2 3 4 .2 = 8 3
CM
2 tháng 6 2017
Đáp án C
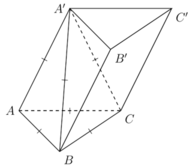
Từ giả thiết suy ra tứ diện A'ABC đều có cạnh a nên có thể tích là
V A ' A B C = a 3 2 12
Khi đó
V A B C . A ' B ' C ' = d A ' , A B C . S A B C = 3 V A ' A B C = a 3 2 4
CM
6 tháng 3 2018
Chọn C
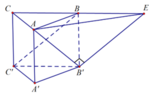
Gọi E là điểm đối xứng của C qua điểm B. Khi đó tam giác ACE vuông tại A.
⇒ A E = 4 a 2 - a 2 = a 3
Mặt khác, ta có BC'=B'E=AB' nên tam giác AB'E vuông cân tại B'.
⇒ A B ' = A E 2 = a 3 2 = a 6 2
Suy ra: A A ' = a 6 2 2 - a 2 = a 2 2
Vậy V = a 2 2 . a 2 3 4 = a 3 6 8
CM
20 tháng 7 2017
Đáp án B
Ta thấy A ' . A B C là tứ diện đều cạnh a → V A ' . A B C = a 3 2 12
Vậy thể tích khối lăng trụ A B C . A ' B ' C ' là V = 3 × V A ' . A B C = 3. a 3 2 12 = a 3 2 4