Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.

Do tam giác ABC đều có cạnh bằng a 3 nên
S A B C = a 3 2 . 3 4 = 3 a 2 3 4
Tam giác A'BC vuông tại A nên:
A ' B 2 = A A ' 2 + A B 2 ⇒ A A ' = A ' B 2 - A B 2 = 3 a 2 - a 3 2 = a 6
Vậy
V A B C . A ' B ' C ' = A A ' . S A B C = a 6 . 3 a 2 3 4 = 9 2 a 3 4

Chọn D.
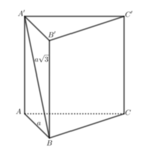
Do tam giác A'AB vuông tại A nên theo pytago ta có
![]()
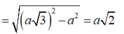
Lại có tam giác ABC vuông cân tại B nên
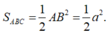
Thể tích khối lăng trụ đã cho
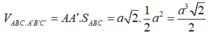

Phương pháp:
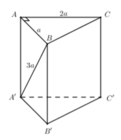
Sử dụng công thức tính thể tích lăng trụ V = S đ á y . h
Cách giải:
Trong tam giác vuông A'AB có:
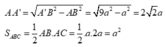
Vậy ![]()
Chọn: C

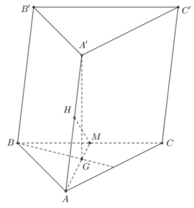
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và \(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam gaics vuông AA'H:
\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{3a}{2}\)
\(V=A'A.S_{ABC}=\dfrac{3a}{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{3}}{8}\)

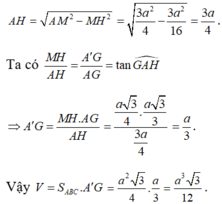
Đáp án C
Từ giả thiết suy ra tứ diện A'ABC đều có cạnh a nên có thể tích là
V A ' A B C = a 3 2 12
Khi đó
V A B C . A ' B ' C ' = d A ' , A B C . S A B C = 3 V A ' A B C = a 3 2 4