CMR: Trong một tam giác cân, đường trung tuyến xuất phát từ đỉnh vừa là đường phân giác của góc ở đỉnh và ngược lại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2018
Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD
Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
TN
2 tháng 4 2022
đường phân giác của góc ở đỉnh vừa là đường trung tuyến xuất phát từ đỉnh
MT
7 tháng 12 2016
Để mik giúp bạn nha Ngọc Hàn Băng Nhi!
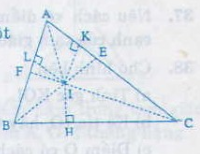
GT : ∆ABC
Hai phân giác BE, CF cắt nhau tại I
AI là tia phân giác của góc A
KL: IH = IK = IL
- Vì I nằm trên tia phân giác BE của góc B nên IL = IH (1) (theo định lí 1 về tính chất của tia phân giác).- Tương tự, ta có IK = IH (2).
- Từ (1) và (2) suy ra IK = IL (= IH), hay I cách đều hai cạnh AB, AC của góc A. Do đó I nằm trên tia phân giác của góc A (theo định lí 2 về tính chất của tia phân giác), hay AI là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
Tóm lại, ba đường phân giác của tam giác ABC cùng đi qua điểm I và điểm này cách đều ba cạnh của tam giác, nghĩa là : IH = IK = IL.
Đây là chỉ là hướng dẫn thui( Do gõ nhìu mỏi tay wá!) Có gì bạn tự triểm khai ra nhé! Chúc bạn học tốt!
DH
19 tháng 5 2017
Vì tam giác ABC cân tại A nên góc ABC= góc ACB(theo tính chất của tam giác cân)
Xét tam giác ABD và tam giác ACD ta có:
góc BAD=góc CAD(gt); AB=AC(gt); góc ABD=góc ACD(cmt)
Do đó tam giác ABD= tam giác ACD(g.c.g)
=> BD=CD=> AD là trung tuyến của cạnh BC của tam giác ABC(đpcm)
Chúc bạn học tốt!!!
20 tháng 2 2018
Xét tam giác ABC cân tại A, đường phân giác AH.
Xét tam giác BAH và tam giác CAH có:
AB=AC (do tam giác ABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}=\frac{\widehat{A}}{2}\)
AH chung
=> \(\Delta BAH=\Delta CAH\left(c.g.c\right)\)
=> \(\widehat{AHB}=\widehat{AHC}\)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)(kề bù)
=>\(\widehat{AHB}=\widehat{AHC}=\frac{180^o}{2}=90^o\)
=>AH L BC
Ngược lại c/m tương tự
3 tháng 4 2022
bạn tham khảo link này nha:https://hoc24.vn/hoi-dap/tim-kiem?id=137279&q=Ch%E1%BB%A9ng%20minh%20%3A%20trong%20m%E1%BB%99t%20tam%20gi%C3%A1c%20c%C3%A2n%2C%20%C4%91%C6%B0%E1%BB%9Dng%20ph%C3%A2n%20gi%C3%A1c%20xu%E1%BA%A5t%20ph%C3%A1t%20t%E1%BB%AB%20%C4%91%E1%BB%89nh%20%C4%91%E1%BB%93ng%20th%E1%BB%9Di%20l%C3%A0%20%C4%91%C6%B0%E1%BB%9Dng%20trung%20tuy%E1%BA%BFn%20%E1%BB%A9ng%20v%E1%BB%9Bi%20c%E1%BA%A1nh%20%C4%91%C3%A1y.
NT
1
1 tháng 5 2018
Giả sử \(\Delta ABC\)cân tại A có AM là trung tuyến .
Xét \(\Delta AMB\)và \(\Delta AMC\)có :
AB = AC ( gt )
AM ( cạnh chung )
BM = CM ( gt )
Suy ra : \(\Delta AMB\)= \(\Delta AMC\)( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
Từ đó suy ra ; AM là tia phân giác của \(\Delta ABC\)
19 tháng 9 2023
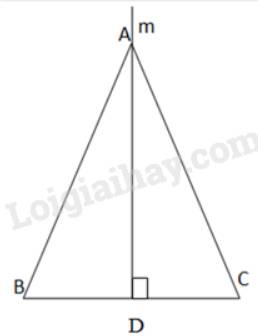
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.
\( \Rightarrow \) AD là đường trung tuyến của BC.
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {ADC} = {90^0}\\AD:chung\\BD = CD\left( {gt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow AB = AC\)(2 cạnh tương ứng)
\( \Rightarrow \Delta ABC\)cân tại A (đpcm).
vì ΔABC cân tại A
=>AB=AC
\(\widehat{B}=\widehat{C}\)
Xét Δ ABH va Δ ACH
AB=AC (cmt)
\(\widehat{B}=\widehat{C}\)(cmt)
HB=HC (vì AH là trung tuyến của Δ ABC)
=> Δ ABH =Δ ACH (c-g-c)
=> \(\widehat{A_1}=\widehat{A_2}\)(2 cạnh tương ứng)
=> AH là phân giác của góc A (đpcm)