Cho hai đường thẳng d1:x+y+2=0, d2:x-3y+1=0.
a) Tìm tọa độ điểm M trên d1 biết M cách d2 một khoảng = 3Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với m = 2 thì d 1 : y = 2x + 3; d 2 : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
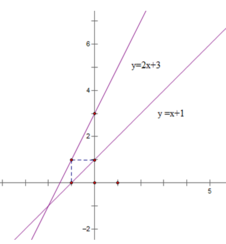
Gọi A ( x 0 ; y 0 ) là tọa độ giao điểm của d1 và d2
Khi đó:
( y 0 = 2 x 0 + 3 và y 0 = x 0 + 1
⇒ 2xo + 3 = x 0 + 1 ⇔ x 0 = -2
⇒ y 0 = x 0 + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d 1 và d 2 là (-2; -1)

M thuộc (d1) nên M(1-2t;1+t)
Theo đề, ta có: d(M;d2)=d(M;d3)
=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)
=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|
=>|-2t+3|=|-11t+3|
=>-2t+3=-11t+3 hoặc -2t+3=11t-3
=>t=0 hoặc t=6/13
=>M(1;1); M(1/13; 19/13)

Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2

1: Để hai đường thẳng cắt nhau thì
2m+1<>m+2
hay m<>1

b: Phương trình hoành độ giao điểm là:
x+1=-x+3
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
hay y=2

\(d_1:mx+y=3m-1.\\ \Leftrightarrow-mx+3m-1=y.\)
\(d_2:x+my=m+1.\\ \Leftrightarrow my=-x+m+1.\\\Leftrightarrow y=\dfrac{-x}{m}+\dfrac{m}{m}+\dfrac{1}{m}.\Leftrightarrow y=-\dfrac{1}{m}x+1+\dfrac{1}{m}.\)
Thay m = 2 vào phương trình đường thẳng d1 ta có:
\(-2x+3.2-1=y.\\ \Leftrightarrow-2x+5=y.\)
Thay m = 2 vào phương trình đường thẳng d2 ta có:
\(y=-\dfrac{1}{2}x+1+\dfrac{1}{2}.\\ \Leftrightarrow y=\dfrac{-1}{2}x+\dfrac{3}{2}.\)
Xét phương trình hoành độ giao điểm của d1 và d2 ta có:
\(-2x+5=\dfrac{-1}{2}x+\dfrac{3}{2}.\\ \Leftrightarrow\dfrac{-3}{2}x=-\dfrac{7}{2}.\\ \Leftrightarrow x=\dfrac{7}{3}.\)
\(\Rightarrow y=\dfrac{1}{3}.\)
Tọa độ giao điểm của d1 và d2 khi m = 2 là \(\left(\dfrac{7}{3};\dfrac{1}{3}\right).\)
a: Vì M nằm trên d1 nên M(x;-x-2)
Theo đề, ta có: \(\dfrac{\left|x\cdot1-3\cdot\left(-x-2\right)+1\right|}{\sqrt{1^2+\left(-3\right)^2}}=3\)
\(\Leftrightarrow\left|x+3x+6+1\right|=3\sqrt{10}\)
\(\Leftrightarrow\left|4x+7\right|=3\sqrt{10}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3\sqrt{10}-7}{4}\\x=\dfrac{-3\sqrt{10}-7}{4}\end{matrix}\right.\)