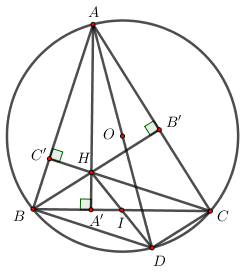
Cho tam giác ABC có 3 góc nội tiếp trong đường tròn tâm O. Kẻ các đường cao BB' và CC' (B' thuộc cạnh AC, C' thuộc cạnh AB). Đường thẳng B'C' cắt đường tròn tâm O tại hai điểm M và N (theo thứ tự N, C', B', M).
a) Chứng minh tứ giác BC'B'C là tứ giác nội tiếp
b) Chứng minh AM = AN
c) AM2 = AC'. AB


Lời giải:
a)
Xét tứ giác $BC'B'C$ có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)
\(\Rightarrow BC'B'C\) là tứ giác nội tiếp.
b)
Vì $BC'B'C$ nội tiếp nên \(\widehat{AC'B'}=\widehat{ACB}\)
\(\Leftrightarrow \widehat{NAC'}+\widehat{ANC'}=\widehat{ACB}\)
\(\Leftrightarrow \widehat{NAB}+\widehat{ANM}=\widehat{ACB}\)
\(\Leftrightarrow \frac{1}{2}\text{cung}(NB)+\frac{1}{2}\text{cung} (AM)=\frac{1}{2}\text{cung} (AB)=\frac{1}{2}(\text{cung (AN)+ cung (NB)})\)
\(\Leftrightarrow \frac{1}{2}\text{cung (AM)}=\frac{1}{2}\text{cung (AN)}\Rightarrow AM=AN\)
c)
Xét tam giác $ANC'$ và $ABN$ có:
\(\left\{\begin{matrix} \text{chung góc A}\\ \widehat{ANC'}=\frac{1}{2}\text{cung (AM)}=\frac{1}{2}\text{cung (AN)}=\widehat{ABN}\\ \end{matrix}\right.\)
\(\Rightarrow \triangle ANC'\sim \triangle ABN(g.g)\Rightarrow \frac{AN}{AB}=\frac{AC'}{AN}\)
\(\Leftrightarrow AN^2=AC'AB\).
Mà \(AM=AN\Rightarrow AM^2=AC'.AB\) (đpcm)
Cảm ơn rất nhiều ạ!