giup em vs a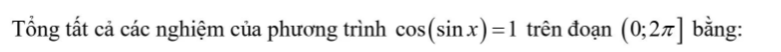
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



5: Để A nguyên thì \(x^2-4+6⋮x+2\)
\(\Leftrightarrow x+2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(x\in\left\{-1;-3;0;-4;1;-5;4;-8\right\}\)

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.






Ta có: ΔABC đều
mà BP,CM là các đường trung tuyến
nên BP,CM là các đường cao
Xét tứ giác BMPC có
\(\widehat{BMC}=\widehat{BPC}=90^0\)
nên BMPC là tứ giác nội tiếp
hay B,M,P,C cùng thuộc 1 đường tròn

1) \(\sqrt{\dfrac{1}{200}}\) 2) \(\dfrac{5}{1-\sqrt{6}}\)
\(=\sqrt{\dfrac{1^2}{10^2.2}}\) \(=\dfrac{1-\sqrt{6}+4+\sqrt{6}}{1-\sqrt{6}}\)
\(=\dfrac{1}{10\sqrt{2}}\) \(=1+\dfrac{4+\sqrt{6}}{1-\sqrt{6}}\)
Bài 2:
1. \(\sqrt{2x-5}=7\) ĐKXĐ: \(x\ge\dfrac{5}{2}\)
<=> 2x - 5 = 72
<=> 2x - 5 = 49
<=> 2x = 54
<=> x = 27 (TM)
2. \(3+\sqrt{x-2}=4\) ĐKXĐ: \(x\ge2\)
<=> \(\sqrt{x-2}=1\)
<=> x - 2 = 1
<=> x = 3 (TM)
3. \(\sqrt{x^2-2x+1}=1\)
<=> \(\sqrt{\left(x-1\right)^2}=1\)
<=> \(|x-1|=1\)
<=> \(\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4. \(\sqrt{x^2-4x+4}=1\)
<=> \(\sqrt{\left(x-2\right)^2}=1\)
<=> \(|x-2|=1\)
<=> \(\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5. \(\sqrt{4x^2+1-4x}=\sqrt{x^2+16+8x}\)
<=> \(\left(\sqrt{4x^2+1-4x}\right)^2=\left(\sqrt{x^2+16+8x}\right)^2\)
<=> \(|4x^2+1-4x|=|x^2+16+8x|\)
<=> \(\left[{}\begin{matrix}4x^2+1-4x=x^2+16+8x\\4x^2+1-4x=-\left(x^2+16+8x\right)\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}4x^2-x^2-4x-8x+1-16=0\\4x^2+1-4x=-x^2-16-8x\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}3x^2-12x-15=0\\5x^2+4x+17=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}3x^2+3x-15x-15=0\\VNghiệm\end{matrix}\right.\)
<=> 3x(x + 1) - 15(x + 1) = 0
<=> (3x - 15)(x + 1) = 0
<=> \(\left[{}\begin{matrix}3x-15=0\\x+1=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
 gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ







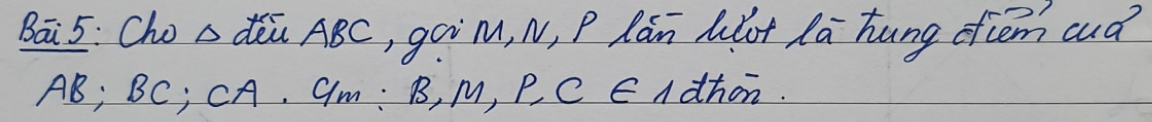

Đặt \(y=sinx\left(y\in\left[-1;1\right]\right)\).
\(cos\left(sinx\right)=1\)
\(\Leftrightarrow cosy=1\)
\(\Leftrightarrow y=k2\pi\)
Vì \(y\in\left[-1;1\right]\Rightarrow-1\le k2\pi\le1\Leftrightarrow-\dfrac{1}{2\pi}\le k\le\dfrac{1}{2\pi}\)
\(\Rightarrow k=0\)
\(\Rightarrow y=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
\(\Leftrightarrow k\in\left\{0;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pi\\x=2\pi\end{matrix}\right.\)
\(\Rightarrow S=3\pi\)
x=0 thì ko phải vi phạm đk rồi ạ