Cho tam giác ABC. điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song với AB cắt AC ở D. Đường thẳng đi qua M và song song với AC cắt AB ở E. Gọi I là trung điểm của DE . Chứng minh rằng :
a, AD=ME
b, Ba điểm A,I,M thẳng hàng .
@Vương Đại Nguyên ( Giú mình nha bạn :33 )

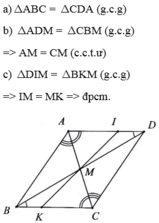
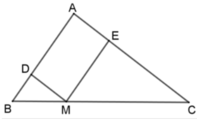
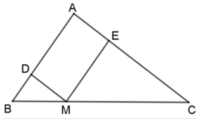
a) Xét tam giác AED và tam giác MDE , có :
ED : chung
góc AED = góc MDE ( AB // DM )
góc ADE = góc MED ( EM // AC )
=> tam giác AED = tam giác MDE ( g-c-g )
=> AD = ME ( hai cạnh tương ứng )
Vậy AD = ME
b) Vì góc AIE + góc AID = 180 độ ( hai góc kề bù ) mà góc AID + góc DIM = 180 độ => ba điểm A , I , M thẳng hảng
Vây ba điểm A , I , M thẳng hảng