Người ta thả 1kg nước đá ở nhiệt độ - 300C vào một bình chứa 3kg nước ở nhiệt độ 480C.
a. Xác định nhiệt độ của hỗn hợp khi cân bằng nhiệt.
b. Sau đó người ta thả vào bình một cục nước đá khác ở 00C gồm một mẩu chì ở giữa có khối lượng 10 gam và M gam nước đá bao quanh mẩu chì. Khối lượng M của cục nước đá đó phải tối thiểu bằng bao nhiêu để mẩu chì không bị chìm.
Cho cđá = 2100J/kg.K; cn = 4200J/kg.K; cchì = 130J/kg.K; đá = 3,4.105J/kg; Dđá = 900kg/m3; Dn = 1000kg/m3; Dchì = 11500kg/m3. Bỏ qua sự trao đổi nhiệt giữa bình và môi trường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nhiệt lượng thu vào để nóng chảy bình nước đá(\(0^oC\)): \(Q_1=m_1c_1\left(0-t_1\right)+m_1\lambda=1\cdot2100\cdot30+1\cdot340000=403000J\)
Nhiệt lượng nước đá tỏa ra để hạ nhiệt độ xuống \(0^oC\):
\(Q_2=m_2c_2\left(t_2-0\right)=2\cdot4200\cdot\left(48-0\right)=403200J\)
\(\Rightarrow Q_2>Q_1\),ta có nhiệt độ chung khi cân bằng nhiệt:
Nhiệt lượng 1kg nước thu vào:
\(Q'_1=m_1c_2\left(t-0\right)=4200t\left(J\right)\)
Nhiệt lượng 2kg nước tỏa ra: \(Q'_2=m_2c_2\left(t_2-t_1\right)=2\cdot4200\cdot\left(48-t\right)=403200-8400t\left(J\right)\)
Cân bằng nhiệt:
\(Q_1+Q'_1=Q'_2\Rightarrow40300+4200t=403200-8400t\)
\(\Rightarrow t=0,016^oC\)
Vậy nhiệt độ hỗn hợp khi cân bằng nhiệt là \(t=0,016^oC\)

Đáp án: D
- Nhiệt lượng do nước đá thu vào để tan chảy hoàn toàn ở 0°C là:
![]()
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0°C là:
![]()
- Ta thấy Q t h u > Q t ỏ a chứng tỏ chỉ 1 phần nước đá bị tan ra.
- Như vậy khi cân bằng nhiệt, hỗn hợp gồm cả nước và nước đá.
- Hay khi cân bằng nhiệt, nhiệt độ của hỗn hợp là t = 0 0 C

Đáp án: C
- Giả sử nhiệt độ của hỗn hợp sau khi cân bằng là 0 0 C
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Ta thấy Q t h u < Q t ỏ a chứng tỏ nước đá bị tan ra hoàn toàn.
- Gọi nhiệt độ hỗn hợp sau khi cân bằng là t 0 C (t > 0)
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C , tan hết tại 0 0 C và tăng lên đến t 0 C là:
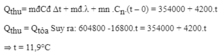

nhiệt lượng cần thiết để tăng nước đá từ - 30 đến 0 là \(Q_1=1.2100.30=63000\left(J\right)\)
nhiệt lượng cần thiết để làm tan 1 kg đá là \(Q_2=1.34.10^4=340000\left(J\right)\)
Nhiệt lượng tỏa ra khi nước hạ từ 48 đến 0 là \(Q_3=2.4200.48=403200\left(J\right)\)
Vì \(Q_3>Q_2+Q_1\) nên đá tan hết, nhiệt đọ cân bằng lớn hơn 0
Nhiệt độ cân bằng của hỗn hợp là \(\text{⇔ m1c1 ( t1 − t ) = Q1 + Q2 + m2c1 ( t − t0 ) }\)
\(\text{⇔ 2.4200. ( 48 − t ) = 63000 + 340000 + 1.4200 ( t − 0 )}\)
\(\text{⇔ 8400 ( 48 − t ) = 403000 + 4200 t }\)
\(\text{⇔ 403200 − 8400 t = 403000 + 4200 t }\)
\(\text{⇔ 200 = 12600 t ⇒ t = 0 , 016^0C }\)

Tóm tắt:
m1 = 2kg
c1= 4200J/kg.K
t1 =48oC
m2 = 1kg
c2= 1800J/kg.K
t2 =-30oC
t=?
Giải:
Nhiệt độ cân bằng của hỗn hợp là:
Q1=Q2 (phương trình cân bằng nhiệt)
m1.c1.△t1=m2.c2.△t2
m1.c1.(t1-t)=m2.c2.(t-t2)
m1.c1.t1 - m1.c1.t = m2.c2.t - m2.c2.t2
m1.c1.t1 + m2.c2.t2 = m2.c2.t + m1.c1.t
m1.c1.t1 + m2.c2.t2 = t(m2.c2 + m1.c1)
t = \(\dfrac{m_1.c_1.t_1+m_2.c_2.t_2}{m_1.c_1+m_2.c_2}\)
t=\(\dfrac{2.4200.48+1.1800.\left(-30\right)}{2.4200+1.1800}\)\(\approx\)34,24oC
Đáp số : t \(\approx\)34,24oC
.
chatgpt