Hàm số y=x3-6x2+mx+1 đồng biến trên miền (0; +vô cực) khi giá trị của m là:
A. m nhỏ hơn hoặc bằng 0
B. m lớn hơn hoặc bằng 0
C. m nhỏ hơn hoặc bằng 12
D. m lớn hơn hoặc bằng 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
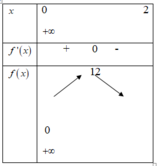
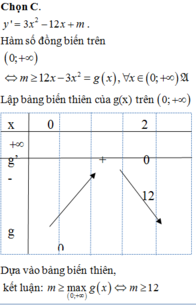
Ta có y ' = 3 x 2 − 12 x + m
Hàm số đồng biến trên y = f ' x
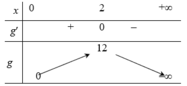
Ta có f ' x = − 6 x + 12 ⇒ f ' x = 0 ⇔ x = 2 . Ta có bảng biến thiên hàm số f(x) như trên
Từ bảng biến thiên, suy ra f x 0 ; + ∞ ≤ 12 ⇒ m ≥ f x 0 ; + ∞ ⇔ m ≥ 12

Chọn C.
![]() . Hàm số đồng biến trên (0;+
∞
)
. Hàm số đồng biến trên (0;+
∞
)![]() )
)
Lập bảng biến thiên của g(x) trên (0;+ ∞ )
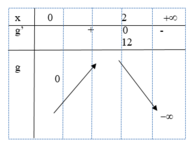
Dựa vào bảng biến thiên, kết luận ![]()
Lập bảng biến thiên của g(x) trên

Chọn D.
Cách 1: Tập xác định: D = R. Ta có ![]()
+) Trường hợp 1:
![]()
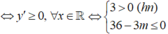
![]()
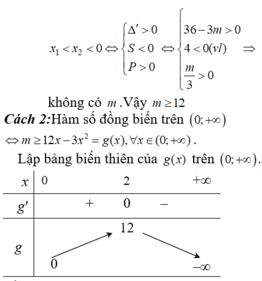
+) Trường hợp 2: Hàm số đồng biến trên (0; +∞) ⇔ y' = 0 có hai nghiệm x1; x2 thỏa mãn x1 < x2 ≤ 0(*)
-) Trường hợp 2.1: y’ = 0 có nghiệm x = 0 suy ra m = 0.
Nghiệm còn lại của y’ = 0 là x = 4 (không thỏa (*))
-) Trường hợp 2.2: y’ = 0 có hai nghiệm x1; x2 thỏa mãn:
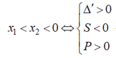
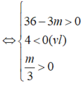
![]()
Kết hợp 2 trường hợp, vậy m ≥ 12
![]()
![]()
![]()

Chọn C.
Ta có: y =
-
x
3
+
6
x
2
+
2
![]()
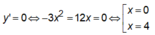
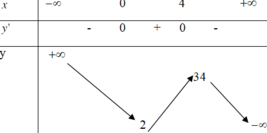
BBT:
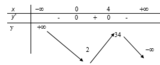
Dựa vào BBT ta thấy hàm số đồng biến trên khoảng (0;4).



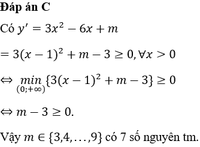
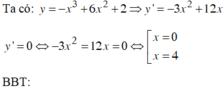
Chọn B