cho hình vuông abcd có
góc a và b bằng 15 độ
chứng minh tam giác icd là tam giác cân am giác đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

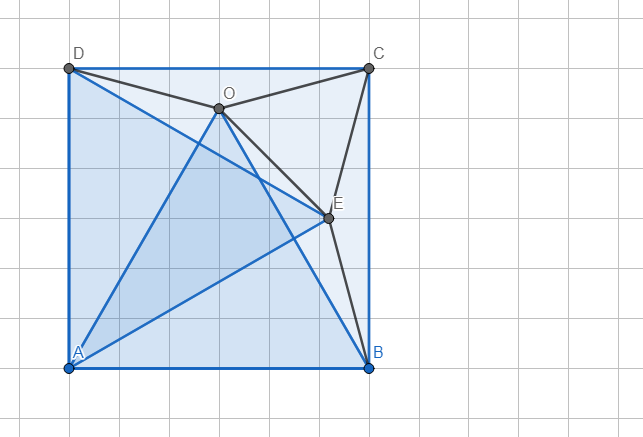
*Dựng △ADE đều.
\(\widehat{ODC}=\widehat{OCD}=15^0\Rightarrow\)△DOC cân tại O.
\(\Rightarrow OD=OC;\widehat{DOC}=180^0-2\widehat{ODC}=180^0-2.15^0=150^0\)
\(\widehat{BAE}=\widehat{CDE}=90^0-\widehat{ADE}=90^0-60^0=30^0\)
\(AB=AE=DE=DC=AD\).
\(\Rightarrow\)△DCE cân tại D, △ABE cân tại A.
\(\Rightarrow\widehat{DCE}=\widehat{ABE}=\dfrac{180^0-\widehat{BAE}}{2}=\dfrac{180^0-30^0}{2}=75^0\).
\(\Rightarrow\widehat{ECB}=\widehat{EBC}=90^0-\widehat{DCE}=90^0-75^0=15^0\)
\(\widehat{OCE}=90^0-\widehat{OCD}-\widehat{BCE}=90^0-15^0-15^0=60^0\)
△DOC và △BEC có: \(\widehat{ODC}=\widehat{EBC}=15^0;\widehat{OCD}=\widehat{ECB}=15^0;DC=BC\)
\(\Rightarrow\)△DOC=△BEC (g-c-g)
\(\Rightarrow OD=BE=OC=EC\)
\(\Rightarrow\)△OCE cân tại C mà \(\widehat{OCE}=60^0\)
\(\Rightarrow\)△OCE đều.
\(\widehat{OEB}=360^0-\widehat{OEC}-\widehat{BEC}=360^0-60^0-150^0=150^0\)
\(OE=CE=EB\Rightarrow\)△OEB cân tại E.
\(\Rightarrow\widehat{OBE}=\dfrac{180^0-\widehat{OEB}}{2}=\dfrac{180^0-150^0}{2}=15^0\)
\(\widehat{OBA}=90^0-\widehat{OBE}-\widehat{CBE}=90^0-15^0-15^0=60^0\)
Mà △OAB cân tại O \(\Rightarrow\)△OAB đều.

Câu a (1,0đ) Chứng minh :![]() ABD =
ABD = ![]() ACE
ACE
Xét ![]() ABD và
ABD và![]() ACE :có AB=AC (cạnh bên
ACE :có AB=AC (cạnh bên ![]() cân);
cân); ![]() =
=![]() (góc đáy
(góc đáy![]() cân);BD=CE (gt) (0,25đ) x3=(0,75đ)
cân);BD=CE (gt) (0,25đ) x3=(0,75đ)
Vậy ![]() ABD =
ABD = ![]() ACE(cgc) (0,25đ)
ACE(cgc) (0,25đ)
Câu b (0,75đ) Chứng minh đúng ![]() vuông AMD =
vuông AMD = ![]() vuông ANE vì có AD = AE;
vuông ANE vì có AD = AE; ![]()
(do ![]() ABD =
ABD =![]() ACE) (0,5đ)
ACE) (0,5đ)
Kết luận ![]() AMD =
AMD =![]() ANE và suy ra AM =AN) (0,25đ)
ANE và suy ra AM =AN) (0,25đ)
Câu c (0,75đ): Chứng minh đúng ![]() vuông BMD =
vuông BMD =![]() vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
Lập luận chứng minh được ![]() rồi suy ra
rồi suy ra ![]() KDE cân tại K (1)(0,25đ)
KDE cân tại K (1)(0,25đ)
Từ ![]() lập luận để
lập luận để ![]()
![]() (2)
(2)
Kết hợp (1)và (2) ![]()
![]() KDE đều )(0,25đ)
KDE đều )(0,25đ)

a) Xét tam giác ABD và tam giác ACE có:
AB = AC (Vì tam giác ABC cân tại A)
\(\widehat{ABC}=\widehat{ACB}\)(vì tam giác ABC cân tại A)
BD = CE (gt)
Do đó tam giác ABD = tam giác ACE(cgc)
b) Ta có: tam giác ABD = tam giác ACE (cmt)
\(\Rightarrow\)AD = AE (hai cạnh tương ứng) (1)
\(\Rightarrow\widehat{BAD}=\widehat{CAE}\)(hai góc tương ứng) (2)
Từ (1) và (2) \(\Rightarrow\) tam giác vuông AMD = tam giác vuông ANE (ch-gn)
\(\Rightarrow\)AM = AN (hai cạnh tương ứng)
c) Trong tam giác ABC có góc BAC=120 độ
\(\Rightarrow\)Góc ABC = góc ACB = \(\frac{180-120}{2}\)= 30 độ
Trong tam giác vuông BMD có góc MBD = 30 độ \(\Rightarrow\widehat{MDB}=60\)độ
Tương tự: Ta được, trong tam giác vuông NCE có góc NEC =60 độ
\(\Rightarrow\)\(\widehat{MDB}=\widehat{NEC}\)(=60 độ)
Mặt khác: \(\widehat{MDB}=\widehat{EDK}\left(đđ\right)\)
\(\widehat{NEC}=\widehat{DEK}\left(đđ\right)\)
\(\Rightarrow\widehat{EDK}=\widehat{DEK}\)(=60 độ)
\(\Rightarrow\widehat{DKE}=180-\left(60\times2\right)=60\)độ
\(\Rightarrow\)Trong tam giác DKE có 3 góc EDK;DEK;DKE cùng bằng 60
Hay tam giác DKE đều.
a) Xét hai tam giác ABD và ACE ta có
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\left(gt\right)\)
BD = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
b) Ta có: \(\Delta ABD=\Delta ACE\)(câu a)
\(=>\hept{\begin{cases}\widehat{BAD}=\widehat{EAC}\\AD=AE\end{cases}}\)(cặp góc và cặp cạnh tương ứng)
Xét hai tam giác vuông AMD và ANE ta có
AD = AE (cmt)
\(\widehat{MAD}=\widehat{EAN}\left(cmt\right)\)
Do đó: \(\Delta AMD=\Delta ANE\left(c.h-g.n\right)\)
=> AM =AN (cặp cạnh tương ứng)
c) Trong \(\Delta ABC\)cân tại A ta có: \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{BAC}}{2}=\frac{180^o-120^0}{2}=30^o\)
Trong \(\Delta MDB\)vuông tại M ta có: \(\widehat{BDM}=90^o-\widehat{DBM}=90^o-30^o=60^o\)
Ta lại có: \(\widehat{ABC}=\widehat{ACB}\left(gt\right)\)
=> \(\widehat{MDB}=\widehat{NEC}\)(vì cùng bù với \(\widehat{ABC}\))
mà \(\hept{\begin{cases}\widehat{BDM}=\widehat{KDE}\left(đđ\right)\\\widehat{NEC}=\widehat{DEK}\left(đđ\right)\end{cases}}\)
=> \(\widehat{KDE}=\widehat{KED}=60^o\)(1)
Trong \(\Delta DKE\)có: \(\widehat{KDE}+\widehat{KED}+\widehat{DKE}=180^o\)
hay \(60^o+60^o+\widehat{DKE}=180^o\)
\(120^o+\widehat{DKE}=180^o\)
\(\widehat{DKE}=180^o-120^o\)
\(\widehat{DKE}=60^o\)(2)
Từ (1) và (2) => \(\Delta DKE\)là tam giác đều
P/s: k hộ thần :3
Văn hay là toán đấy!!?!?