Giải giúp mình 2 câu này với huhu, làm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2

b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cos2x-\dfrac{1}{2}sin2x=-cosx\)
\(\Leftrightarrow cos\left(2x+\dfrac{\pi}{6}\right)=cos\left(x+\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\pi+k2\pi\\2x+\dfrac{\pi}{6}=-x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{6}+k2\pi\\x=-\dfrac{7\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
c.
\(\Leftrightarrow2cos4x.sin3x=2sin4x.cos4x\)
\(\Leftrightarrow cos4x\left(sin4x-sin3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\sin4x=sin3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{\pi}{2}+k\pi\\4x=3x+k2\pi\\4x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=k2\pi\\x=\dfrac{\pi}{7}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
2.
\(f\left(x\right)=\dfrac{1}{2}-\dfrac{1}{2}cos2x-\dfrac{\sqrt{3}}{2}sin2x-5\)
\(=-\dfrac{9}{2}-\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)\)
\(=-\dfrac{9}{2}-cos\left(2x-\dfrac{\pi}{3}\right)\)
Do \(-1\le-cos\left(2x-\dfrac{\pi}{3}\right)\le1\Rightarrow-\dfrac{11}{2}\le y\le-\dfrac{7}{2}\)
\(y_{min}=-\dfrac{11}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=1\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
\(y_{max}=-\dfrac{7}{2}\) khi \(cos\left(2x-\dfrac{\pi}{3}\right)=-1\Rightarrow x=\dfrac{2\pi}{3}+k\pi\)

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm

Câu 1.
\(R_N=R_1+R_2=2+3=5\Omega\)
\(I_1=I_2=I=\dfrac{\xi}{r+R_N}=\dfrac{9}{1+5}=1,5A\)
\(U_N=I\cdot R_N=1,5\cdot5=7,5V\)
\(U_1=I_1\cdot R_1=1,5\cdot2=3V;U_2=7,5-3=4,5V\)
\(P_1=I_1^2\cdot R_1=1,5^2\cdot2=4,5W\)
\(P_2=1,5^2\cdot3=6,75W\)

Đường thẳng d có 1 vtpt là \(\left(1;-2\right)\)
Đường thẳng \(d'\) vuông góc d nên có 1 vtpt là (2;1) (đảo thứ tự tọa độ vtpt của d và đảo dấu 1 trong 2 vị trí tùy thích)
Phương trình d':
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)

7:
a: \(P=\left(1:\dfrac{x-x+1}{\sqrt{x}+\sqrt{x-1}}-\dfrac{x-1-2}{\sqrt{x-1}-\sqrt{2}}\right)\cdot\left(\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)\(=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\dfrac{\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\)
\(=-\dfrac{\left(\sqrt{x}-\sqrt{2}\right)}{\sqrt{x}}\)
b: Khi x=3-2căn 2 thì \(P=-\dfrac{\sqrt{2}-1-\sqrt{2}}{\sqrt{2}-1}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)

b: (d) có hệ số góc bằng 1 nên (d): y=x+b
f(2)=-1/2*2^2=-2
Thay x=2 và y=-2 vào (d), ta được:
b+2=-2
=>b=-4
a: 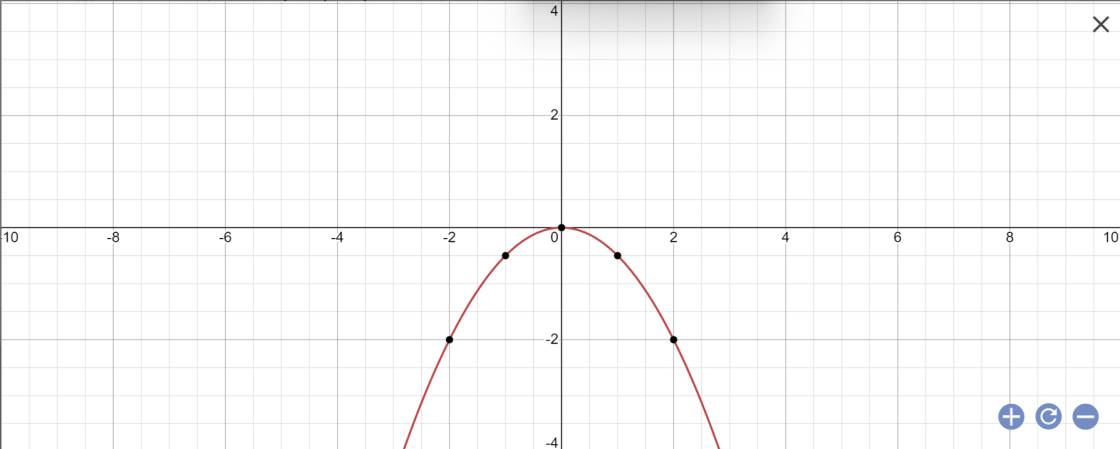






 Giúp mình giải 2 câu này với. Mình cảm ơn
Giúp mình giải 2 câu này với. Mình cảm ơn
a.
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+sinx.cosx\right)=1\)
Đặt \(sinx+cosx=t\) \(\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t\left(1+\dfrac{t^2-1}{2}\right)=1\)
\(\Leftrightarrow t^3+t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2+t+2\right)=0\)
\(\Leftrightarrow t=1\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)
b.
Đặt \(sinx-cosx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1-2sinx.cosx\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Phương trình trở thành:
\(t^3=1+\dfrac{1-t^2}{2}\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)