ai có lòng hảo tâm gửi cho mình mấy cái bất đẳng thức dùng để tìm GTLN hoặc GTNN và cách c/m BĐT đó đi!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 8 2018
\(|a+b|\ge0\)\(\Rightarrow GTNN|a+b|=0\)
\(|a|\ge0;|b|\ge0\Rightarrow a=0;b=0\)
\(C=3|x+2|+|3x+1|\)
\(\hept{\begin{cases}|x+2|\ge0\Rightarrow3|x+2|\ge0\\|3x+1|\ge0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}GTNN3|x+2|=0\\GTNN|3x+1|=0\end{cases}}\Rightarrow C=0\)
\(\hept{\begin{cases}3|x+2|=0\Rightarrow|x+2|=0\Rightarrow x+2=0\Rightarrow x=-2\\|3x+1|=0\Rightarrow3x+1=0\Rightarrow3x=-1\Rightarrow x=\frac{-1}{3}\end{cases}}\)
\(\Rightarrow x\)không thể có 2 giá trị.\(\Rightarrow\orbr{\begin{cases}3|x+2|=0\\|3x+1|=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-2\\x=\frac{-1}{3}\end{cases}}\)
Xét \(x=-2\)và\(x=\frac{-1}{3}\):
\(x=-2\Rightarrow3|x+2|=0\Rightarrow C=|3x+1|\)
\(C1=|3x+1|\)
\(=|3.\left(-2\right)+1|\)
\(=|\left(-6\right)+1|\)
\(=|-5|\)
\(=5\)
\(x=\frac{-1}{3}\Rightarrow|3x+1|=0\Rightarrow C=3|x+2|\)
\(C2=3|x+2|\)
\(=3|\frac{-1}{3}+2|\)
\(=3|\frac{-1+6}{3}|\)
\(=3|\frac{5}{3}|\)
\(=\frac{3.5}{3}\)
\(=5\)
\(C1=C2=5\)
\(\Rightarrow GTNNC=5\)
CT
17 tháng 3 2019
nhân chéo lên
nhân a+b+c từ 9/a+b+c sang vế trái
vế phải còn 9
sau đó nhân vế trái ra
sử dụng bdt cosi là ra nha bn
9 tháng 8 2016
Vd : \(x^2+6x+10\)
Ta có : 10 không căn được
Mà : \(x^2+2.x.3+3^2\)
Nhưng 32 chỉ là 9 nên ta cộng thêm 1 ở vế sau
\(\left(x^2+2.x.3+3^2\right)+1\)
\(\left(x+3\right)^2+1\)
Dư 1 ở ngoài :
Vì \(\left(x+3\right)^2\ge0\)
=> \(\left(x+3\right)^2+1\ge1\)
=> GTNN là 1
Khi ( x + 3 ) = 0
x = -3
Khi
9 tháng 8 2016
Giải
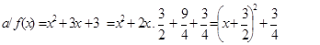
Ta có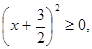 
nên 
Vậy: f(x) đạt GTNN bằng 
khi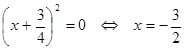 
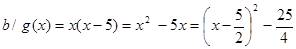
Ta có 
nên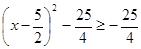 
Vậy: g(x) đạt GTNN bằng 
khi 
AH
Akai Haruma
Giáo viên
8 tháng 7 2017
Lời giải:
Tìm max:
Áp dụng BĐT Bunhiacopsky:
\(M^2=(2x+\sqrt{5-x^2})^2\leq (2^2+1)(x^2+5-x^2)=25\)
\(\Rightarrow M\leq 5\) hay \(M_{\max}=5\Leftrightarrow x=2\)
Tìm min:
Ta thấy \(5-x^2\geq 0\Rightarrow x^2\leq 5\rightarrow x\geq -\sqrt{5}\)
Do đó: \(M=2x+\sqrt{5-x^2}\geq =-2\sqrt{5}+0=-2\sqrt{5}\)
\(\Rightarrow M_{\min}=-2\sqrt{5}\Leftrightarrow x=-\sqrt{5}\)
25 tháng 7 2018
I don't now
mik ko biết
sorry
......................
26 tháng 7 2018
1. \(2ab\le\frac{\left(a+b\right)^2}{2}\le a^2+b^2\) ( \(\forall a;b\))
2. \(\frac{a}{b}+\frac{b}{a}\ge2\)( \(\forall a;b>0\))
3. \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)\(\left(a;b>0\right)\)
4. \(\frac{1}{ab}\ge\frac{4}{\left(a+b\right)^2}\) \(\left(a;b>0\right)\)
5. \(\left(a^2+b^2\right)\left(c^2+d^2\right)\ge\left(ac+bd\right)^2\)
6. \(a^2+b^2+c^2\ge ab+bc+ca\)
7. \(3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\)
8. \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) \(\left(a;b;c>0\right)\)
9. \(\frac{a^2}{x}+\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}\)\(\left(x;y>0\right)\)
10. \(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{\left(a+b+c\right)^2}{x+y+z}\) \(\left(x;y;z>0\right)\)
Search mạng ^-^.^-^
tìm trên nó rối tùm lum lắm, bạn cho mình cái tên cx dc, mình lên tìm