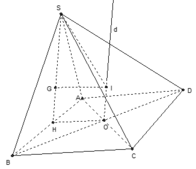
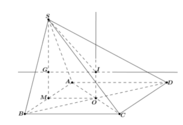
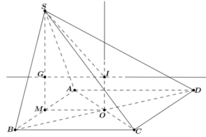
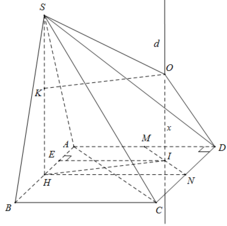
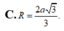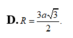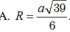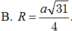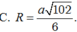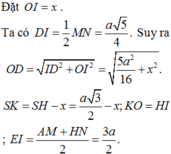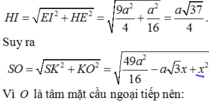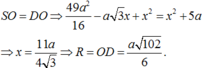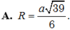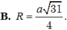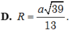Cho hình chóp SABCD. Đáy ABCD là hình vuông cạnh bằng a tâm O, SAB là tam giác đều có trọng tâm G và nằm trên mặt phẳng vuông góc với (ABCD). Tính bán kính R mặt cầu ngoại tiếp hình chóp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 6 2019
Đáp án D
Gọi H là trung điểm của AB, do tam giác SAB đều nên SH ⊥ AB mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD)
Gọi O là tâm của hình vuông ABCD, d là đường thẳng qua O và song song SH thì d ⊥ (ABCD) hay d là trục đường tròn ngoại tiếp hình vuông ABCD
Trong mặt phẳng (SAB) từ G kẻ đường thẳng vuông góc với (SAB) cắt d tại I thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính R = IS.
CM
15 tháng 10 2017
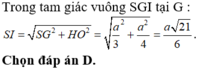
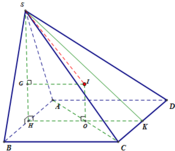
Gọi H là trung điểm của AB, suy ra A H ⊥ A B C D .
Gọi G là trọng tâm tam giác ∆SAB và O là tâm hình vuông ABCD.
Từ G kẻ GI//HO suy ra GI là trục đường tròn ngoại tiếp tam giác ∆SAB và từ O kẻ OI//SH thì OI là trục đường tròn ngoại tiếp hình vuông ABCD.
Ta có hai đường này cùng nằm trong mặt phẳng và cắt nhau tại I.
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
R = S I = S G 2 + G I 2 = a 21 6 .
Suy ra thể tích khối cầu ngoại tiếp khối chóp S.ABCD là V = 4 3 π R 3 = 7 21 54 π a 3
Đáp án A
CM
24 tháng 9 2019
Chọn đáp án A
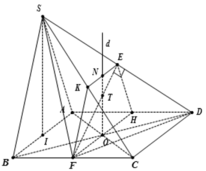
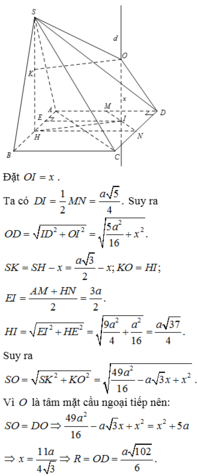
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
Bán kính mặt cầu là
+ Xét tam giác vuông TOB vuông tại B, ta có
CM
7 tháng 11 2017
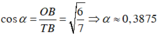
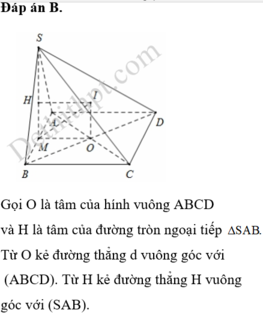
Đáp án B.
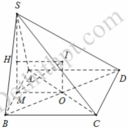
Gọi O là tâm của hính vuông ABCD và H là tâm của đường tròn ngoại tiếp Δ S A B . Từ O kẻ đường thẳng d vuông góc với (ABCD). Từ H kẻ đường thẳng H vuông góc với (SAB).
Ta có d ∩ Δ = I ⇒ I A = I B = I C = IS ⇒ I là tâm đường tròn ngoại tiếp khối chóp S . A B C D ⇒ R = I A = O I 2 + O A 2 .
Mà O I = H M = H B 2 − M B 2 với M là trung điểm của AB.
Xét Δ S A B cân tại S, có A B sin A S B ^ = 2 r
⇒ H B = r = 2 a 2. sin 120 0 = 2 a 3 .
Khi đó O I = 2 a 3 2 − a 2 = a 3 ⇒ R = a 3 2 + a 2 2 = a 21 3 .
