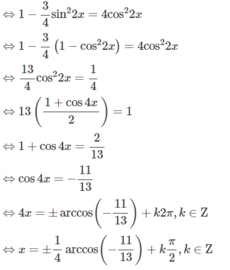giải phương trình
sin8x -cos6x = \(\sqrt{3}\)( sin6x + cos8x )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2020
c/
\(\Leftrightarrow\sqrt{3}sin3x-cos3x=sin2x-\sqrt{3}cos2x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x-\frac{1}{2}cos3x=\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=sin\left(2x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=2x-\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{6}=\pi-2x+\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{3\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2020
e/
\(\Leftrightarrow\frac{1}{2}sin8x-\frac{\sqrt{3}}{2}cos8x=\frac{\sqrt{3}}{2}sin6x+\frac{1}{2}cos6x\)
\(\Leftrightarrow sin\left(8x-\frac{\pi}{3}\right)=sin\left(6x+\frac{\pi}{6}\right)\)
\(\Rightarrow\left[{}\begin{matrix}8x-\frac{\pi}{3}=6x+\frac{\pi}{6}+k2\pi\\8x-\frac{\pi}{3}=\pi-6x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{28}+\frac{k\pi}{7}\end{matrix}\right.\)
LT
1
19 tháng 8 2021
M = 3(sin^8x-cos^8x) + 4(cos^6x-2sin^6x)+6sin^4x
Ta có:
sin^8(x) - cos^8(x) = [sin^4(x) ]² - [cos^4(x)]²
= (sin²x + cos²x)(sin²x -cos²x).[ sin^4(x) + cos^4(x) ]
= (sin²x -cos²x)[ sin^4(x) + cos^4(x) ]
= sin^6(x) - cos^6(x) + sin²x.cos^4(x) -cos²x.sin^4(x)
Lúc đó M viết lại là:
M = 3.[sin^6(x) - cos^6(x) + sin²x.cos^4(x) -cos²x.sin^4(x) ] + 4.[ cos^6(x) -2sin^6(x) ] + 6sin^4(x)
M = -5sin^6(x) + cos^6(x) -3sin^4(x).cos²x + 3sin²x.cos^4(x) +6sin^4(x)
M = -3sin^(6)x - 3cos²x.sin^4(x) + cos^4(x).sin²x + cos^6(x) - 2sin^6(x) + 2sin²x.cos^4(x) + 6sin^4(x)
M = -3sin^4(x).(sin²x + cos²x ) + cos^4(x).[sin²x + cos²x ] -2sin²x.[sin^4(x) - cos^4(x) ] + 6sin^4(x)
M = 3sin^4(x) + cos^4(x) -2sin²x.[sin²x - cos²x]
M = 3sin^4(x) + cos^4(x) -2sin^4(x) + 2sin²x.cos²x
M = sin^4(x) + 2sin²x.cos²x + cos^4(x)
M = [sin²x + cos²x ]² = 1
M
14 tháng 6 2020
\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)
PT
1
CM
8 tháng 11 2017
sin 6 x + cos 6 x = 4 cos 2 2 x ⇔ sin 2 x + cos 2 x 3 - 3 sin 2 x . cos 2 x ( sin 2 x + cos 2 x ) = 4 cos 2 2 x
