Xác định phần dư R(x) của phép chia:
P(x)=1+x+x9+x25+x49 +x81 cho x³-x. Rồi tính R(701,4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 11 2018
Do \(x^3-x\) có bậc 3 => R(x) có bậc tối đa là bậc 2
\(\Rightarrow\)Đặt \(R\left(x\right)=ax^2+bx+c\) và gọi Q(x) là phần thương số, ta được:
\(x^{81}+x^{49}+x^{25}+x^9+x+1=\left(x^3-x\right)Q\left(x\right)+ax^2+bx+c\) (1)
Cho \(x=0\Rightarrow\) (1)\(\Leftrightarrow1=c\)
Cho \(x=1\) thì \(\left(1\right)\Leftrightarrow6=a+b+1\Rightarrow a+b=5\) (2)
Cho \(x=-1\) thì \(\left(1\right)\Leftrightarrow-4=a-b+1\Rightarrow a-b=-5\) (2)
Từ (2) và (3) có hệ \(\left\{{}\begin{matrix}a+b=5\\a-b=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=0\\b=5\end{matrix}\right.\)
Vậy phần dư là \(R\left(x\right)=5x+1\)
19 tháng 9 2023
a)
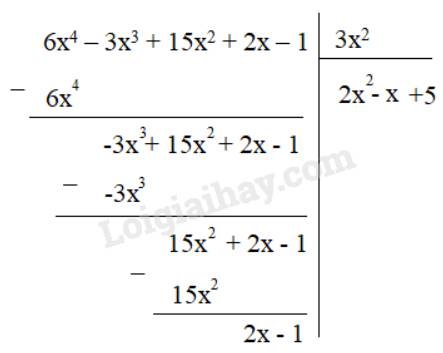
Thương Q(x) = 2x2 – x + 5
Dư R(x) = 2x – 1
Ta có: F(x) = 3x2 . (2x2 – x + 5) + 2x – 1
b)
Thương Q(x) = 4x2 + 2x – 2
Dư R(x) = -x – 1
Ta có: F(x) = (3x2 + x + 1) . (4x2 + 2x – 2) – x – 1
Gọi thương của phép chia \(P\left(x\right)\) cho \(x^3-x\) là \(Q\left(x\right)\)
Vì đa thức chia có bậc 3 nên đa thức dư có bậc không quá 2.
Ta có: \(P\left(x\right)=1+x+x^9+x^{25}+x^{49}+x^{81}=Q\left(x\right).x\left(x-1\right)\left(x+1\right)+ax^2+bx+c\)Với \(x=1\) ta có: \(a+b+c=6\) (1)
Với \(x=-1\) ta có: \(a-b+c=-4\) (2)
Với \(x=0\) ta có: \(c=1\)
Thế \(c=1\) vào (1) và (2) ta có:
\(\left\{{}\begin{matrix}a+b=5\\a-b=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=5\end{matrix}\right.\)
\(\Rightarrow R\left(x\right)=5x+1\)