Chứng minh rằng nếu O là một điểm bất kì nằm trong tứ giác ABCD sao cho các diện tích tam giác ABO, BCO, CDO và DAO bằng nhau thì O phải thuộc 1 trong 2 đường chéo AC và BD .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 6 2018
Bạn tự vẽ hình nha
- Nếu O thuộc BD ta hiển nhiên có điều phải chứng minh
- Nếu O không thuộc BD
Giả sử BD cắt OA, OC lần lượt tại E, F
Từ D và B kẻ các đường vuông góc DH, BK xuống AO với H,K thuộc AO
Ta có : \(S_{OAD}=S_{OAB}\)mà hai tam giác này có chung đáy OA ⇒DH=BK
Xét tam giác DHE vuông tại H và tam giác BKE vuông tại K có:
DH=BK
\(\widehat{EDH}=90^o-\widehat{DEH}=90^o-\widehat{BEK}=\widehat{EBK}\)
\(\Rightarrow\Delta EDH=\Delta EBK\)
\(\Rightarrow DE=EB\)
Tương tự \(S_{ODC}=S_{OBC}\Rightarrow DF=FB\)
\(\Rightarrow E\equiv F\)
O, C, F thẳng hàng ; O, E, A thẳng hàng ; E = F ⇒⇒ A, C, O, E thẳng hàng. Vậy O thuộc đường chéo AC.
1 tháng 7 2018
kuihihuolu uh
| ]o-][[p[po[]\[]iy89t768r67r675r65r67r5676666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666 |
CM
23 tháng 10 2019
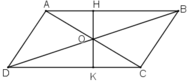
Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.
Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB ⇒ O, H, K thẳng hàng.
Do đó:
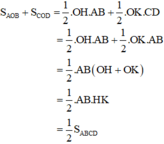
Mà SABCD = SAOB + SBOC + SCOD + SDOA
Do đó SAOB + SCOD = SBOC + SDOA.
GH
20 tháng 6 2023
Có:
\(\dfrac{S_{DAO}}{S_{ABO}}=\dfrac{DO}{BO}=\dfrac{S_{CDO}}{S_{BCO}}\) , tức là \(S_{DAO}.S_{BCO}=S_{ABO}.S_{CDO}\)
Do đó:
\(S_{ABO}.S_{BCO}.S_{CDO}.S_{DAO}=\left(S_{DAO}+S_{BCO}\right)^2\)
Vậy tích các số đo diện tích của các tam giác ABO, BCO, CDO, DAO là một số chính phương.
6 tháng 1 2017
Qua O vẽ OH ⊥ AB và OK ⊥ AD ⇒ OH ⊥ DC, OK ⊥ BC
Gọi I, L lần lượt là giao điểm của OK, OH với DC, BC. Ta có:
+ S_ABCD = AB.IH = BC.KL
+ S_ABO = 1/2 AB.OH và S_CDO = 1/2 DC.OI
⇒ S_ABO + S_CDO = 1/2 AB.OH + 1/2 DC.OI
= 1/2 AB.OH + 1/2 AB.OI
= 1/2 AB (OH + OI) = 1/2 AB.IH = 1/2 S_ABCD (1)
+ S_BCO = 1/2 BC.OL và S_DAO = 1/2 AD.OK
⇒ S_BCO + SDAO = 1/2 BC.OL + 1/2AD.OK
= 1/2 BC.OL + 1/2BC.OK
= 1/2BC(OL + OK) = 1/2 BC.KL = 1/2S_ABCD (2)
Từ (1) và (2) ta có: S_ABO + S_CDO = S_BCO + S_DAO
Q
22 tháng 4 2017
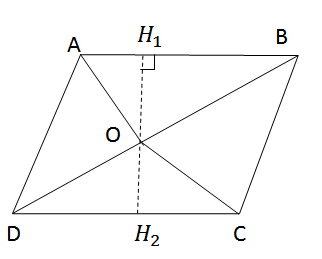
Từ O lẻ đường thẳng d vuông góc với AB ở H1, cắt CD ở H2.
Ta có OH1 ⊥ AB
Mà AB // CD
Nên OH2 ⊥ CD
Do đó: SABO + SCDO = \(\dfrac{1}{2}\)OH1 . AB + \(\dfrac{1}{2}\) OH2 . CD
= \(\dfrac{1}{2}\)AB (OH1 + OH2)
= \(\dfrac{1}{2}\)AB . H1 . H2
Nên \(S_{ABO}+S_{CDO}=\dfrac{1}{2}S_{ABCD}\) ( 1)
Tương tự \(S_{BCO}+S_{DAO}=\dfrac{1}{2}S_{ABCD}\) (2)
Từ (1) và (2) suy ra :
\(S_{ABO}+S_{CDO}=S_{BCO}+S_{DAO}\)
XO
7 tháng 6 2021
Ta có SABO = OE.AB : 2
Vì \(\hept{\begin{cases}AB//CD\\\widehat{AEO}=90^{\text{o}}\end{cases}}\Rightarrow\widehat{CFO}=90^{\text{o}}\)
=> SCDO = OF.CD : 2 = OF.AB : 2
=> SABO + SCDO = EF.AB : 2 = \(\frac{1}{2}S_{ABCD}\)(Vì EF là đường cao hình bình hành ABCD => SABCD = EF.AB)
Tương tự ta được
SBCO + SDAO = HK.BC : 2 = \(\frac{1}{2}S_{ABCD}\)(HK đường cao hình bình hành ABCD => SABCD = HK.BC)
=> SABO + SCDO = SBCO + SDAO (= \(\frac{1}{2}S_{ABCD}\)) => ĐPCM