Cho hàm số y=(3x+6)/(x-1) (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến song song với đường thẳng d: 3x+4y-21
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 4 2019
Ta có y ' = x 2 - 4 x + 3 . Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.
Xét y' = 3 <=> x 2 - 4 x = 0
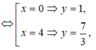
Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1
Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là
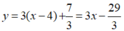
Chọn đáp án D.
CM
13 tháng 3 2019
Vì phương trình tiếp tuyến song song với đường thẳngy =-3x + 1nên nó có hệ số góc là -3
Do đó f ' x = 3 x 2 − 10 x = − 3 ⇔ 3 x 2 − 10 x + 3 = 0
⇔ x = 1 3 x = 3
Với x = 1 3 thì y 0 = 40 27 Vậy phương trình tiếp tuyến là: y = − 3 x − 1 3 + 40 27 = − 3 x + 67 27
Với x=3thì y 0 = - 16 Vậy phương trình tiếp tuyến là: y = -3(x- 3) – 16 = - 3x – 7
Chọn đáp án C
CM
12 tháng 6 2019
Đáp án B
Phương trình tiếp tuyến tại x 0 ; y 0 có hệ số góc là k = y ' = − 3 x − 1 2
Để tiếp tuyến tại x 0 ; y 0 song song với đường thẳng d : y = − 3 x − 1 thì
k = − 3 x − 1 2 = − 3 ⇔ x − 1 2 = 1 ⇔ x 1 = 2 x 2 = 0 ⇔ y 1 = 5 y 2 = − 1 ⇔ d 1 : y = − 3 x + 11 d 2 : y = − 3 x − 1 ≡ d ( l o a i )
CM
22 tháng 7 2019
Đáp án C
Gọi d là tiếp tuyến của C tại M x 0 ; y 0 thỏa mãn đề bài
Ta có y ' = x 2 − 4 x + 3 ⇒ y ' x 0 = x 0 2 − 4 x 0 + 3 = k d là hệ số góc của d
d / / y = 3 x + 1 ⇒ k d = x 0 2 − 4 x 0 + 3 = 3 ⇔ x 0 = 0 x 0 = 4
Với x 0 = 0 ⇒ M 0 ; 1 ⇒ d : 3 x − 0 + 1 ⇔ d : y = 3 x + 1 ≡ y = 3 x + 1
Với x 0 = 4 ⇒ M 4 ; 7 3 ⇒ d : 3 x − 4 + 7 3 ⇔ d : y = 3 x − 29 3
Vậy d : y = 3 x − 29 3
CM
11 tháng 10 2017
Đáp án C
Gọi d là tiếp tuyến của (C) tại M x 0 ; y 0 thỏa mã đề bài.
Ta có y ' = x 2 − 4 x + 3 ⇒ y ' x 0 = x 0 2 − 4 x 0 + 3 = k d là hệ số góc của d.
d / / y = 3 x + 1 ⇒ k d = 3 ⇔ x 0 2 − 4 x 0 + 3 = 3 ⇔ x 0 = 0 x 0 = 4 .
Với x 0 = 0 ⇒ M 0 ; 1 ⇒ d : y = 3 y − 0 + 1 ⇔ d : y = 3 x + 1 ≡ y = 3 x + 1.
Với x 0 = 4 ⇒ M 4 ; 7 3 ⇒ d : y = 3 y − 4 + 7 3 ⇔ d : y = 3 x − 29 3 .
Suy ra d : y = 3 x − 29 3 .
29 tháng 4 2016
Ta có : \(y'=\frac{x^2-2x}{\left(x-1\right)^2}\)
Gọi \(M\left(x_0;y_0\right)\) là tọa độ tiếp điểm của tiếp tuyến d với (C)
\(d:y=\frac{x_0^2-2_0x}{\left(x_0-1\right)^2}\left(x-x_0\right)+\frac{x_0^2-x_0+1}{x_0-1}\)
a) Vì d song song với đường thẳng \(\Delta:y=\frac{3}{4}x+\frac{1}{4}\) nên ta có :
\(\frac{x_0^2-2_0x}{\left(x_0-1\right)^2}=\frac{3}{4}\Leftrightarrow x_0^2-2_0x-3=0\Leftrightarrow x_0=-1;x_0=3\)
* \(x_0=-1\) phương trình tiếp tuyến : \(y=\frac{3}{4}x-\frac{3}{4}\)
* \(x_0=3\) phương trình tiếp tuyến : \(y=\frac{3}{4}x+\frac{5}{4}\)
b) Đường thẳng \(\Delta_m\) có hệ số góc \(k_m=\frac{1}{m}\)
Số tiếp tuyến thỏa mãn bài toán chính là số nghiệm của phương trình :
\(y'.k_m=-1\Leftrightarrow\frac{m\left(x^2-2x\right)}{\left(x-1\right)^2}=-1\)
\(\Leftrightarrow\left(m+1\right)x^2-2\left(m+1\right)x+1=0\left(1\right)\)
* Nếu m = - 1 suy ra (1) vô nghiệm, suy ra không có tiếp tuyến nào
* Nếu \(m\ne-1\), suy ra (1) có \(\Delta'=m\left(m+1\right)\) và (1) có nghiệm \(x=1\Leftrightarrow m=0\)
+ Khi \(\left[\begin{array}{nghiempt}m>0\\m< -1\end{array}\right.\) suy ra (*) có 2 nghiệm phân biệt nên có 2 tiếp tuyến
+ Khi \(-1< m\le0\) thì (*) vô nghiệm nên không có tiếp tuyến nào
Lời giải:
Ta có \(y=\frac{3x+6}{x-1}\Rightarrow y'=\frac{-9}{(x-1)^2}\)
Gọi tiếp điểm của tiếp tuyến với đồ thị C là \(M\left(x_0,\frac{3x_0+6}{x_0-1}\right)\)
PTTT: \(y=f'(x_0)(x-x_0)+f(x_0)\)
\(\Leftrightarrow y=\frac{-9}{(x_0-1)^2}(x-x_0)+\frac{3x_0+6}{x_0-1}=\frac{-9x}{(x_0-1)^2}+\frac{3x_0^2+12x_0-6}{(x_0-1)^2}\)
Để ĐT trên song song với \(d:3x+4y-21=0\) thì:
\(\frac{-9}{(x_0-1)^2}=\frac{-3}{4}\Leftrightarrow x_0=1\pm 2\sqrt{3}\)
Do đó PTTT là: \(y=\frac{-3x}{4}+\frac{15\pm 12\sqrt{3}}{4}\Leftrightarrow 3x+4y-(15\pm 12\sqrt{3})=0\)