Khi nuôi cá thí nghiệm trong hồ , một nhà sinh vật học thấy rằng: nếu mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau vụ thu hoạch cân nặng :P(n)=480-20n. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau vụ thu hoạch đạt được sản lượng lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 8 2018
Sau một vụ, trung bình số cá trên mỗi đơn vị diện tích mặt hồ cân nặng: f n = n P n = 480 n - 20 n 3
f’(n) = 480 – 40n=0 → n = 12
Bảng biến thiên:
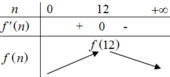
Trên mỗi đơn vị diện tích của mặt hồ, cần thả 12 con cá thì sau một vụ thu hoạch được nhiều gam cá nhất.
Đáp án A
CM
7 tháng 5 2019
Chọn A.
Sau một vụ, trung bình số cá trên mỗi đơn vị diện tích mặt hồ cân nặng:
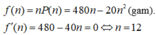
Bảng biến thiên:
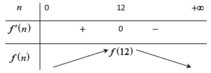
Trên mỗi đơn vị diện tích của mặt hồ, cần thả 12 con cá thì sau một vụ thu hoạch được nhiều gam cá nhất.
14 tháng 5 2019
bạn Đỗ Minh Quang sao nói bạn ý ngu !!! Giỏi thì làm xem
Bài giải :
Một đơn vị diện tích: Thả n con
Sau thu hoạch, mỗi con nặng 480−20n
Do đó, sau thu hoạch, một đơn vị diện tích sẽ thu hoạch được số cân cá là:
A=n(480−20n)
Đến đây có thể dùng 2 cách:
Cách 1: Sử dụng BĐT
Ta có 20A=20n(480−20n). Áp dụng BĐT Cauchy:
20A≤(20n+480−20n2)2=57600
⇔A≤2880. Dấu bằng xảy ra khi 20n=480−20n⇔n=12
Vậy để thu được sản lượng lớn nhất thì n=12
Cách 2: Sử dụng đạo hàm, xét bảng biến thiên ta cũng thu được Amax⇔n=12
Lời giải:
Một đơn vị diện tích: Thả $n$ con
Sau thu hoạch, mỗi con nặng \(480-20n\)
Do đó, sau thu hoạch, một đơn vị diện tích sẽ thu hoạch được số cân cá là:
\(A=n(480-20n)\)
Đến đây có thể dùng 2 cách:
Cách 1: Sử dụng BĐT
Ta có \(20A=20n(480-20n)\). Áp dụng BĐT Cauchy:
\(20A\leq \left (\frac{20n+480-20n}{2}\right)^2=57600\)
\(\Leftrightarrow A\leq 2880\). Dấu bằng xảy ra khi \(20n=480-20n\Leftrightarrow n=12\)
Vậy để thu được sản lượng lớn nhất thì \(n=12\)
Cách 2: Sử dụng đạo hàm, xét bảng biến thiên ta cũng thu được \(A_{\max}\Leftrightarrow n=12\)
sai sai bét