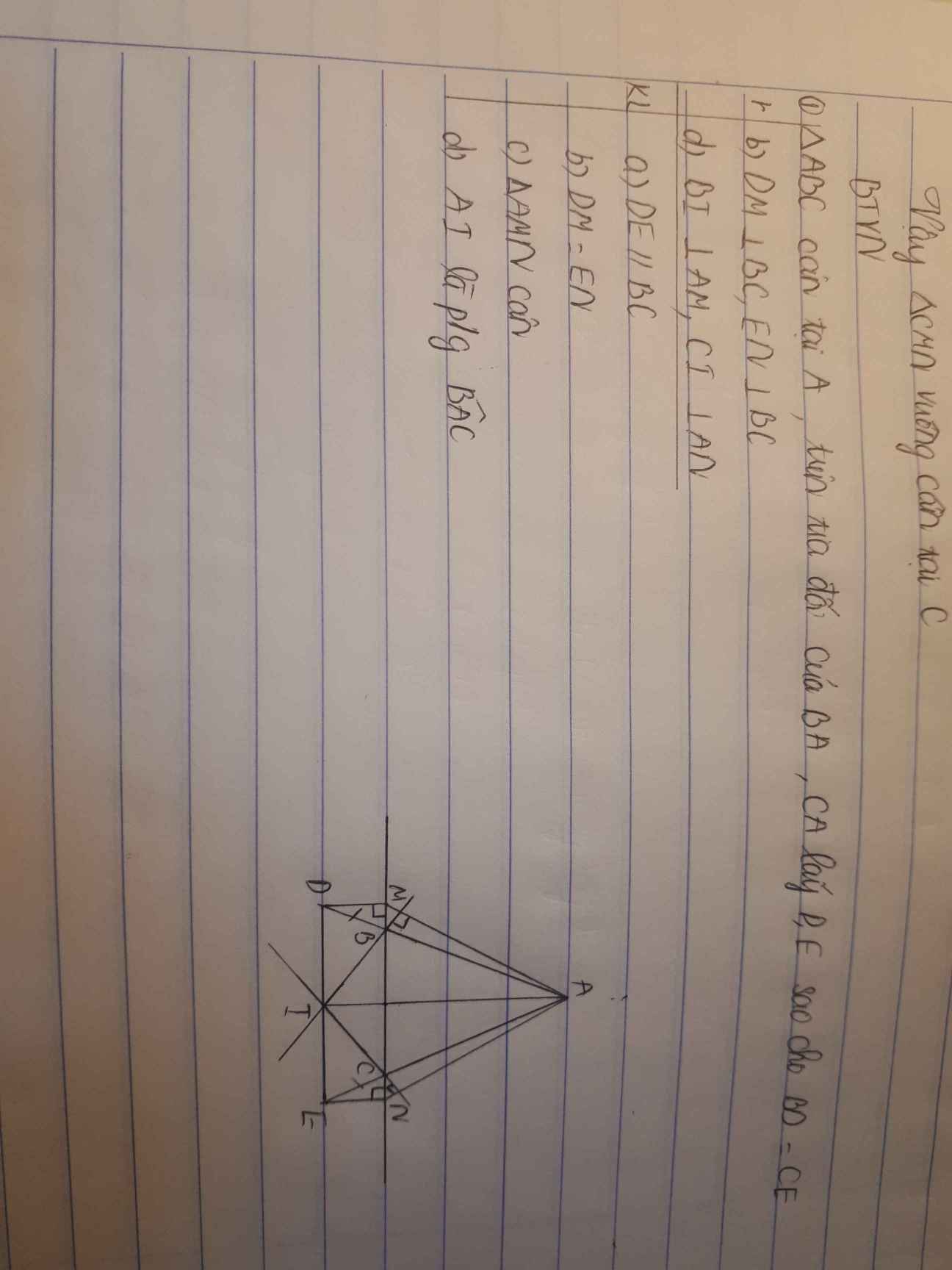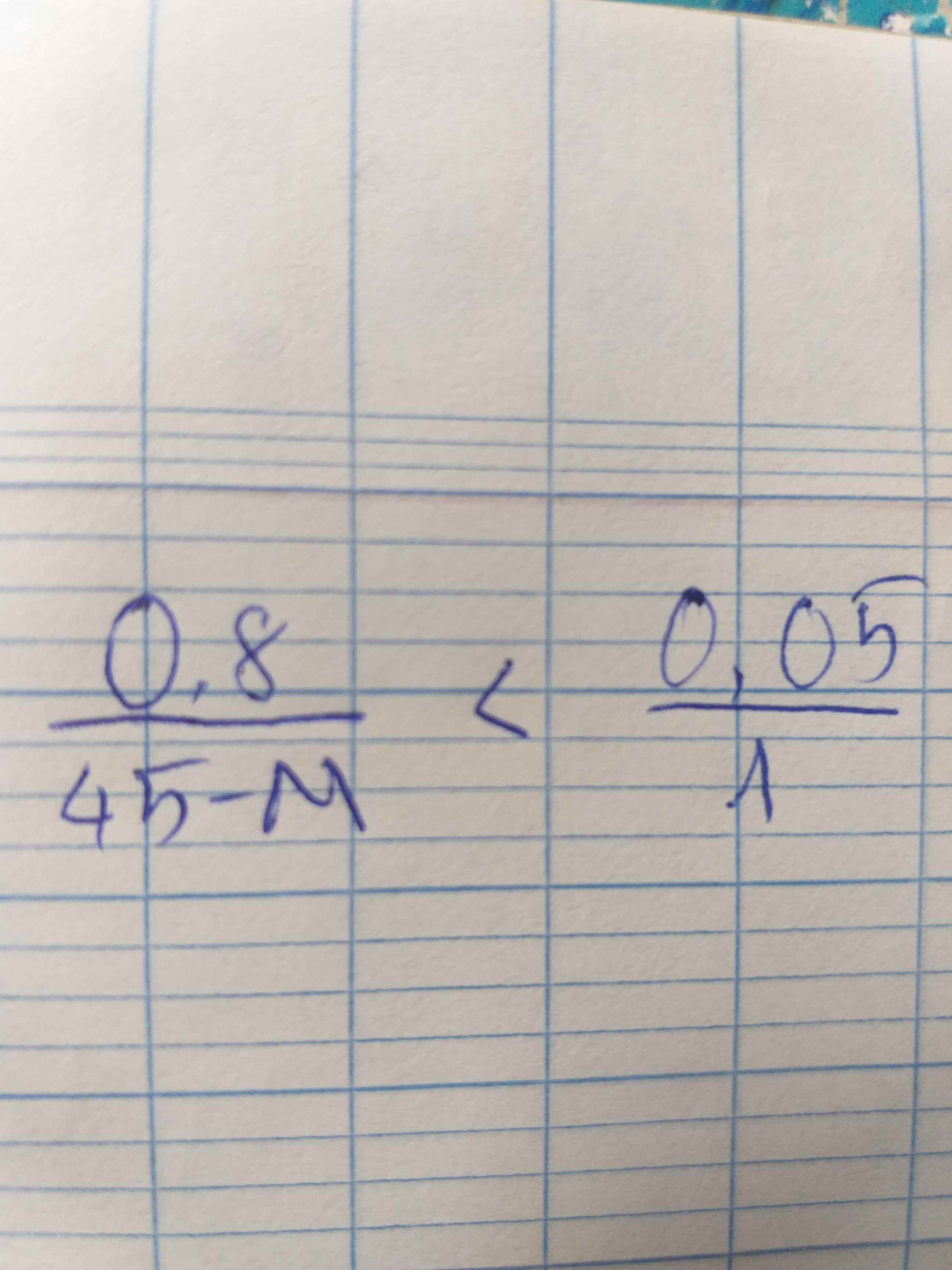Mình chưa hiểu bài này lắm. Có thể giải chi tiết dùm được hông ạ.
Đang cần gấp
Cảm ơn trc nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
13 tháng 11 2021
\(A=-\left(x^2-4x+4\right)-\left(y^2+4y+4\right)+10\\ A=-\left(x-2\right)^2-\left(y+2\right)^2+10\le10\\ A_{max}=10\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)
TM
8 tháng 11 2021
a/ Ta có: \(\begin{matrix}a\text{ // }b\\a\perp AB\end{matrix}\Rightarrow b\perp AB\)
b/ \(\hat{ACD}+\hat{CDB}=180^o\) (trong cùng phía, a // b)
\(\Rightarrow\hat{CDB}=180^o-\hat{ACD}=60^o\)
\(\hat{ACD}+\hat{aCD}=180^o\) (kề bù)
\(\Rightarrow\hat{aCD}=180^o-\hat{ACD}=60^o\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
YV
0
TH
1
16 tháng 6 2023
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
NN
2
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Thực sự mình cũng không hiểu cách giải theo hướng dẫn bạn trích ở trên. Nhưng bạn có thể như sau:
\(\frac{a}{b^2}+\frac{4b}{a^2+b^2}=\frac{2a}{1-a^2}+\frac{4b}{1-b^2}=\frac{2a^2}{a(1-a^2)}+\frac{4b^2}{b(1-b^2)}\)
Áp dụng BĐT AM-GM:
\(2a^2(1-a^2)^2=2a^2(1-a^2)(1-a^2)\leq \left(\frac{2a^2+1-a^2+1-a^2}{3}\right)^3=\frac{8}{27}\)
$\Rightarrow a(1-a^2)\leq \frac{2}{3\sqrt{3}}$
$\Rightarrow \frac{2a^2}{a(1-a^2)}\geq 3\sqrt{3}a^2$
Tương tự: $\frac{4b^2}{b(1-b^2)}\geq 6\sqrt{3}b^2$
Do đó: $\frac{a}{b^2}+\frac{4b}{a^2+b^2}\geq 3\sqrt{3}(a^2+2b^2)=3\sqrt{3}$ (đpcm)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Bài toán này xuất phát từ bài toán quen thuộc:
Cho $a,b,c>0$ thỏa mãn $a^2+b^2+c^2=1$. CMR:
$\frac{a}{b^2+c^2}+\frac{b}{a^2+c^2}+\frac{c}{a^2+b^2}\geq \frac{3\sqrt{3}}{2}$