Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40

a.
ĐKXĐ: \(x\ge2\)
\(\dfrac{\sqrt{x}-\sqrt{x-1}}{\left(\sqrt{x}+\sqrt{x-1}\right)\left(\sqrt{x}-\sqrt{x-1}\right)}+\dfrac{\sqrt{x-1}-\sqrt{x-2}}{\left(\sqrt{x-1}+\sqrt{x-2}\right)\left(\sqrt{x-1}-\sqrt{x-2}\right)}=1\)
\(\Leftrightarrow\dfrac{\sqrt{x}-\sqrt{x-1}}{1}+\dfrac{\sqrt{x-1}-\sqrt{x-2}}{1}=1\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x-2}=1\)
\(\Leftrightarrow\sqrt{x}=1+\sqrt{x-2}\)
\(\Leftrightarrow x=1+x-2+2\sqrt{x-2}\)
\(\Leftrightarrow2\sqrt{x-2}=1\)
\(\Leftrightarrow x-2=\dfrac{1}{4}\)
\(\Rightarrow x=\dfrac{9}{4}\)
b
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}=\dfrac{x-1}{2}\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}=\dfrac{x-1}{2}\)
\(\Leftrightarrow\left|\sqrt{x-1}-1\right|+\left|\sqrt{x-1}+1\right|=\dfrac{x-1}{2}\)
Đặt \(\sqrt{x-1}=t\ge0\Rightarrow\left|t-1\right|+\left|t+1\right|=\dfrac{t^2}{2}\)
TH1: \(0\le t\le1\) pt trở thành:
\(1-t+t+1=\dfrac{t^2}{2}\Rightarrow t^2=4\)
\(\Rightarrow\left[{}\begin{matrix}t=2>1\left(ktm\right)\\t=-2< 0\left(ktm\right)\end{matrix}\right.\)
TH2: \(t>1\) pt trở thành:
\(t-1+t+1=\dfrac{t^2}{2}\Rightarrow t^2=2t\Rightarrow\left[{}\begin{matrix}t=0< 1\left(ktm\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}=2\Rightarrow x=5\)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)

Bạn nên chịu khó gõ đề ra khả năng được giúp sẽ cao hơn.
Câu h của em đây nhé
h, ( 1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1 - \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3-\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{2}\)
= -2

Với m = 3 thì (d): y = 8x - 7
PTHĐGĐ của (P) và (d): \(x^2-8x+7=0\)
Có: \(a+b+c=1+\left(-8\right)+7=0\)
=> PT có 2 nghiệm phân biệt \(x_1=1;x_2=7\)
\(x_1=1\Rightarrow y_1=x_1^2=1^2=1\\ x_2=7\Rightarrow y_2=x_2^2=7^2=49\)
Tọa độ giao điểm của (P) và (d) là: \(\left(1;1\right);\left(7;49\right)\)
b)
PTHĐGĐ của (P) và (d) là:
\(x^2-2\left(m+1\right)x+3m-2=0\)
\(\Delta'=\left(m+1\right)^2-\left(3m-2\right)=m^2+2m+1-3m+2=m^2-m+3\\ =m^2-m+\dfrac{1}{4}+\dfrac{11}{4}=\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall m\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=3m-2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4=20\\ \Leftrightarrow4m^2+2m+8-20=0\\ \Leftrightarrow4m^2+2m-12=0\\ \Leftrightarrow2m^2+m-6=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-2\left(tm\right)\\m=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
Gọi tọa độ của \(\left(P\right),\left(d\right)\) là \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\)
\(a,m=3\)
\(\Rightarrow x^2=2\left(3+1\right)x-3.3+2\)
\(\Rightarrow x^2-8x+7=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Thay \(x=7\) vào \(\left(P\right):y=x^2\Rightarrow y=7^2=49\)
Khi m = 3 thì đường thẳng \(\left(d\right):y=2\left(3+1\right)x-3.3+2=8x-7\)
Thay \(x=1\) vào \(\left(d\right):y=8x-7=8.1-7=1\)
Vậy \(A\left(7;49\right),B\left(1;1\right)\)
\(\Rightarrow y=\left(2m+2\right)x-3m+2\)
\(b,\) Vì \(\left(P\right)\) và \(\left(d\right)\) luôn cắt nhau tại 2 điểm pb A,B \(\forall m\) nên :
\(x^2=2\left(m+1\right)x-3m+2\Leftrightarrow x^2-2\left(m+1\right)x+3m-2\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=3m-2\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=20\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4-20=0\)
\(\Leftrightarrow4m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m=-2\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{2},m=-2\) thì thỏa mãn đề bài.

\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2x-3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3\\3x+2x-3=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-3\\5x=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2.2-3\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)

a.
Khi \(x=4\Rightarrow A=\dfrac{1}{\sqrt{4}}+\dfrac{\sqrt{4}}{\sqrt{4}+1}=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\)
b.
\(B=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\sqrt{x}=x+\sqrt{x}\)
\(\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
c.
\(P=A:B=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P>3\Rightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}>3\)
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\) (do \(\sqrt{x}>0\))
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1\ne0\)
\(\Rightarrow x\ne1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
anh ơi https://hoc24.vn/cau-hoi/giai-phuong-trinh-nghiem-nguyen-saux2x-y20.1353640161947
-> giải thích hộ cái bảng của a tính thế nào vs ạ




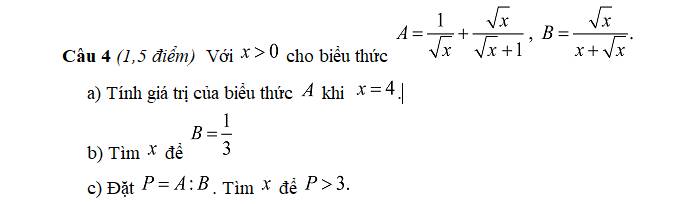
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)