Cho phân số 17/53. Hỏi phải bớt đi ở tử số và mẫu số cùng một số tự nhiên nào để được phân số mới có giá trị 1/4 ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2022
Gọi số cần tìm là x
Theo đề, ta có:
\(\dfrac{7-x}{8+x}=\dfrac{1}{4}\)
=>28-4x=x+8
=>x=4
10 tháng 5 2022
Gọi số cần tìm là \(a\)
Ta có :
\(\dfrac{7-x}{8+x}=\dfrac{1}{4}\)
\(28-4x=x+8\)
\(x=4\).
30 tháng 5 2022
Tổng tử và mẫu của phân số \(\dfrac{49}{119}\) là:
\(49+119=168\)
Tổng tử và mẫu của phân số \(\dfrac{3}{4}\) là:
\(3+4=7\)
Tử số mới của phân số \(\dfrac{49}{119}\) là:
\(\left(168:7\right)\) x \(3=72\)
Số cần thêm vào tử số và bớt đi ở mẫu của phân số \(\dfrac{49}{119}\) là:
\(72-49=23\)
Vậy phải thêm vào tử số và bớt đi ở mẫu số của phân số đó cùng một số tự nhiên là \(23\) để được phân số mới có giá trị bằng \(\dfrac{3}{4}\)
21 tháng 3 2022
Nếu bớt ở TS 3 đơn vị và thêm vào MS 3 đơn vị ta đc PS : 4/16 = 1/4
Vậy phải bớt ở TS 3 đơn vị và thêm vào MS 3 đơn vị
tk cho mình
21 tháng 3 2022
ờm
gọi số chx bt la : x
(7-x) / (13+x) = 1/4
<=> 4 (7-x) / 4 (13+x) = 13+x / 4 (13+x)
<=> 28 - 4x = 13 + x
<=> 28 - 13 = x + 4x
<=> 15 = 5x
<=> x = 3
vay số đó la 3
DD
Đoàn Đức Hà
Giáo viên
20 tháng 9 2021
Khi bớt ở tử số và thêm vào mẫu số cùng một số thì tổng giữa tử số và mẫu số không đổi.
Tổng của tử số và mẫu số là:
\(82+53=135\)
Nếu phân số mới có tử số là \(5\)phần thì mẫu số là \(4\)phần.
Tổng số phần bằng nhau là:
\(5+4=9\)(phần)
Tử số mới là:
\(135\div9\times5=75\)
Số cần tìm là:
\(82-75=7\)
21 tháng 9 2021
Khi bớt ở tử số và thêm vào mẫu số cùng một số thì tổng giữa tử số và mẫu số không đổi.
Tổng của tử số và mẫu số là :
82+53=135.
Nếu phân số mới có tử số là 5 phần thì mẫu số là 4 phần.
Tổng số phần bằng nhau là :
5+4=9 (phần).
Tử số mới là :
135÷9×5=75.
Số cần tìm là :
82-75=7.
Chúc bạn học tốt!!!!!!!!!!.
Tích cho mình nữa nha bạn!!!!!!!!!!.
21 tháng 9 2019
Gọi số tự nhiên đó là a. Theo đề bài ta có :
\(\frac{25}{37-a}=\frac{5}{6}\)
=> \(\frac{25}{37-a}=\frac{25}{30}\)
=> 37 - a = 30
=> a = 37 - 30 = 7
Vậy a = 7
Gọi số phải cộng thêm vào tử số là x, số phải bớt ở mẫu số là x . Theo đề bài ta có :
\(\frac{3}{18}=\frac{3+x}{18-x}=\frac{3}{4}\)
=> 4[3 + x] = 3[18 - x]
=> 12 + 4x = 54 - 3x
=> 4x + 3x = 54 - 12
=> 7x = 42
=> x = 42 : 7 = 6
22 tháng 2 2022
Gọi số tự nhiên cần tìm là a
Theo đề, ta có:
\(\dfrac{17+a}{18-a}=\dfrac{3}{4}\)
=>68+4a=54-3a
=>7a=-14
hay a=-2
22 tháng 3 2022
TỬ BỚT 2
MẪU THÊM 2
HT...........................................................
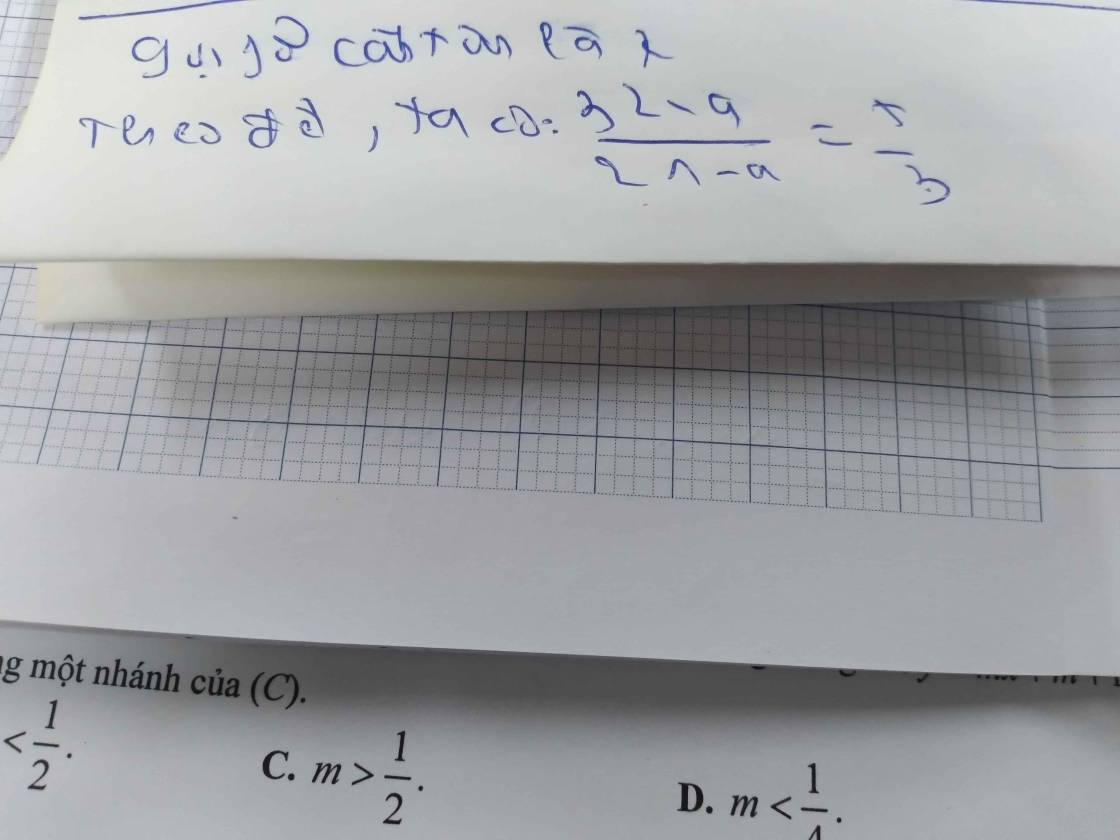
Gọi số tự nhiên cần tìm là a
Theo đề, ta có: \(\dfrac{17-a}{53-a}=\dfrac{1}{4}\)
\(\Leftrightarrow53-a=68-4a\)
\(\Leftrightarrow3a=15\)
hay a=5
\(\dfrac{17-x}{53-x}=\dfrac{1}{4}\Rightarrow x=5\)