Cho 2a2+b2+c2+d2+e2=a(b+c+d+e)
CMR: a=b=c=d=e=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Refer:
a² + b² + c² + d² + e² ≥ a(b + c + d + e)
Ta có: a² + b² + c² + d² + e²= (a²/4 + b²) + (a²/4 + c²) + (a²/4 + d²) + (a²/4 + e²)
Lại có: (a/2 - b)² ≥ 0 <=> a²/4 - ab + b² ≥ 0 <=> a²/4 + b² ≥ ab
Tương tự ta có:. a²/4 + c² ≥ ac.
a²/4 + d² ≥ ad.
a²/4 + e² ≥ ae
--> (a²/4 + b²) + (a²/4 + c²) + (a²/4 + d²) + (a²/4 + e²) ≥ ab + ac + ad + ae
<=> a² + b² + c² + d² + e² ≥ a(b + c + d + e)
=> đpcm.
Dấu " = " xảy ra <=> a/2 = b = c = d = e.

Ta có:
a/(1+b²) = a- ab²/(1+b²) ≥ a - ab/2 (do 1+b² ≥ 2b)
Tương tự ta có:
b/(1+c²) ≥ b- bc/2
c/(1+d²) ≥ c - cd/2
d/(1+a²) ≥ d - ad/2
Cộng vế với vế ta được:
VT = a/(1+b²) + b/(1+c²) + c/(1+d²) + d/(1+a²) ≥ (a+b+c+d) - (ab+bc+cd+da)/2
VT ≥ (a+b+c+d -ab+bc+cd+da)/2 + (a+b+c+d)/2
Ta có:
ab+bc+cd+da = (a+c)(b+d) ≤ [(a+b+c+d)/2]² = 4 = a+b+c+d
=> a+b+c+d ≥ ab+bc+cd+da
=> VT ≥ (a+b+c+d)/2 =2
Dấu = khi a=b=c=d=1

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
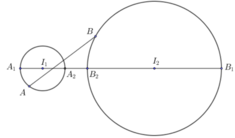
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8


\(\left(2m-a\right)^2+\left(2m-b\right)^2+\left(2m-c\right)^2+\left(2m-d\right)^2+\left(2m-e\right)^2\)
\(=4m^2-4ma+a^2+4m^2-4mb+b^2+4m^2-4mc+c^2+4m^2-4md+d^2+4m^2-4me+e^2\)
\(=20m^2-4m\left(a+b+c+d+e\right)+a^2+b^2+c^2+d^2+e^2\)
\(=20m^2-4m.5m+a^2+b^2+c^2+d^2+e^2\)
\(=a^2+b^2+c^2+d^2+e^2\)

Ta có : a2 + b2 = c2 + d2
⇒a2 + b2 + c2 + d2 = 2 ( a2 + b2 ) ⋮2 nên là hợp số
Ta có : a2 + b2 + c2 + d2 - ( a + b + c + d )
= a ( a - 1 ) + b ( b - 1 ) + c ( c - 1 ) + d ( d - 1 ) ⋮2
⇒a + b + c + d ⋮2 nên cũng là hợp số

\(a^2+b^2+c^2+d^2+1=a\left(b+c+d+1\right)\)
\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4=4ab+4ac+4ad+4a\)
\(\Leftrightarrow a^2-4ab+4b^2+a^2-4ac+4c^2+a^2-4ad+4d^2+a^2-4a+4=0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2b\\a=2c\\a=2d\\a=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=c=d=1\end{matrix}\right.\).
Vậy \(\left(a,b,c,d\right)=\left(2,1,1,1\right)\)
Ta có: \(2a^2+b^2+c^2+d^2+e^2=a\left(b+c+d+e\right)\)
\(\Rightarrow8a^2+4b^2+4c^2+4d^2+4e^2=4ab+4ac+4ad+4ae\)
\(\Rightarrow8a^2+4b^2+4c^2+4d^2+4e^2-4ab-4ac-4ad-4ae=0\)
\(\Rightarrow4a^2+\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)\)
\(+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)=0\)
\(\Rightarrow4a^2+\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2=0\) (1)
Vì \(4a^2\ge0;\left(a-2b\right)^2\ge0;\left(a-2c\right)^2\ge0;\left(a-2d\right)^2\ge0;\left(a-2e\right)^2\ge0\)
với mọi a,b,c,d,e
=> (1) xảy ra \(\Leftrightarrow4a^2=0;\left(a-2b\right)^2=0;\left(a-2c\right)^2=0;\left(a-2d\right)^2=0;\left(a-2e\right)^2=0\)(2)
\(\Rightarrow a=0\) \(\Rightarrow\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left(0-2b\right)^2=0\\\left(0-2c\right)^2=0\\\left(0-2d\right)^2=0\\\left(0-2e\right)^2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}0-2b=0\\0-2c=0\\0-2d=0\\0-2e=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2b=0\\2c=0\\2d=0\\2e=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=0\\c=0\\d=0\\e=0\end{matrix}\right.\Rightarrow a=b=c=d=e=0\)
Vậy a=b=c=d=e=0
\(2a^2+b^2+c^2+d^2+e^2=a\left(b+c+d+e\right)\)
\(\Leftrightarrow2a^2+b^2+c^2+d^2+e^2-a\left(b+c+d+e\right)=0\)
\(\Leftrightarrow2a^2+b^2+c^2+d^2+e^2-ab-ac-ad-ae=0\)
Nhân 2 với hai vế của đẳng thức, ta có:
\(4a^2+2b^2+2c^2+2d^2+2e^2-2ab-2ac-2ad-2ae=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)+\left(a^2-2ad+d^2\right)+\left(a^2-2ae+e^2\right)+\left(b^2+c^2+d^2+e^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(a-d\right)^2+\left(a-e\right)^2+\left(b^2+c^2+d^2+e^2\right)=0\)
Ta gọi biểu thức trên là *
Do \(\left(a-b\right)^2\ge0\) ;
\(\left(a-c\right)^2\ge0\);
\(\left(a-d\right)^2\ge0\);
\(\left(a-e\right)^2\ge0\);
\(\left(b^2+c^2+d^2+e^2\right)\ge0\);
Do các phép tính trên đều là phép cộng, phép trừ
Mà kết quả lại bằng 0
Nên * xảy ra khi a-b=0; a-c=0; a-d=0; a-e=0
và b+c+d+e=0
Mà các số giống nhau hiệu = 0 =>a=b=c=d=e(**)
và các số dương cộng lại bằng 0 =>b,c,d.e=0(***)
Từ (**) và ( ***)=> a=b=c=d=0(dpcm)