Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh bên bằng b, đường cao AH=h. Tính bán kính đường tròn tâm O
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
13 tháng 8 2021
Ta có O là trọng tâm của tg ABC => AO là đường trung tuyến của tg ABC => AO là đường cao của tg ABC (Trong tg cân đường đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao và đường trung trực)
\(\Rightarrow HB=HC=\frac{BC}{2}\)
\(\Rightarrow OH=\frac{AH}{3}=\frac{h}{3}\) (trong tg 3 đường trung tuyến cắt nhau tại 1 điểm gọi là trọng tâm của tg và cách đáy 1 khoảng = 1/3 chiều dài mỗi đường)
Xét tg vuông ABH có
\(BH^2=AB^2+AH^2=b^2+h^2\)
Xét tg vuông OBH có
\(BO=R=\sqrt{BH^2+OH^2}=\sqrt{b^2-h^2+\frac{h^2}{9}}=\frac{1}{3}\sqrt{9b^2-8h^2}\)
TS
14 tháng 7 2021
Kẻ đường kính AD thì góc ACD = 90°
Ta có AC²= AD.AH nên AD = AC²/AH
<=>AD= (10a)²/ 8a=100a/8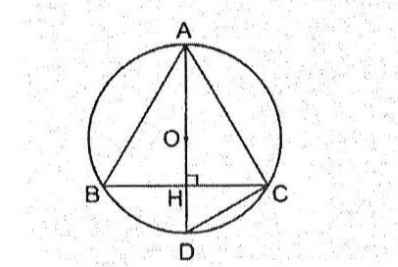
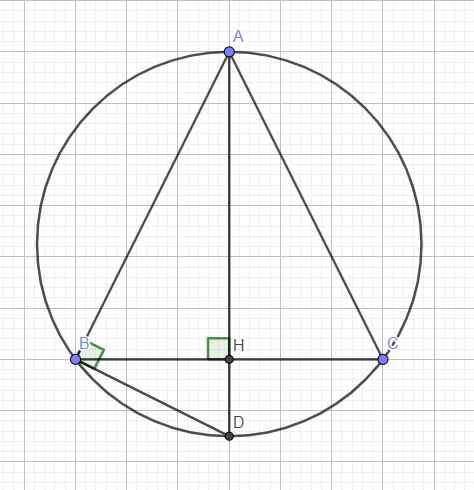
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Kéo dài AH cắt đường tròn tại D \(\Rightarrow\) AD là đường kính
\(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn hay tam giác ABD vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=\dfrac{b^2}{h}\)
\(\Rightarrow2R=\dfrac{b^2}{h}\Rightarrow R=\dfrac{b^2}{2h}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{BC}{2}\cdot h\)
Bán kính là:
\(R=\dfrac{a\cdot b\cdot c}{4\cdot S}=\dfrac{b\cdot b\cdot BC}{4\cdot\dfrac{BC\cdot h}{2}}=\dfrac{b\cdot b\cdot BC}{2\cdot BC\cdot h}=\dfrac{b^2}{2h}\)
Ta có: O là trọng tâm của △ ABC ⇒ AO là đường trung tuyến của △ ABC ⇒ AO là đường cao của △ ABC ( Trong tam giác cân đường đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao và đường trung trực )
⇒ HB = HC = \(\dfrac{BC}{2}\)
⇒ OH = \(\dfrac{AH}{3}=\dfrac{h}{3}\) ( trong tam giác 3 đường trung tuyến cắt nhau tại 1 điểm gọi là trọng tâm của tam giác và cách đáy 1 khoảng = \(\dfrac{1}{3}\) chiều dài mỗi đường )
Xét tam giác vuông ABH có
\(BH^2=AB^2+AH^2=b^2+h^2\)
Xét tam giác vuông OBH có
BO = R = \(\sqrt{BH^2+OH^2}=\sqrt{b^2-h^2+\dfrac{h^2}{9}}=\dfrac{1}{3}\sqrt{9b^2-8h^2}\)