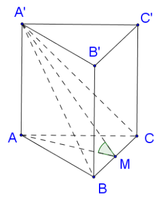
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Góc BC' và mặt (AA'CC') = 30 độ. Tính thể tích lăng trụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
11 tháng 9 2017
Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .


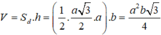




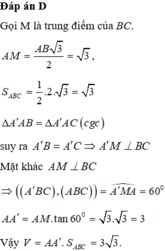


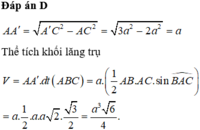


Lời giải:
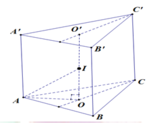
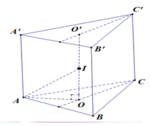
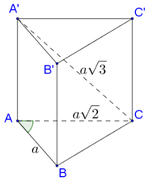
Hình lăng trụ tam giác đều là hình lăng trụ đứng. Kẻ \(BH\perp CA\) thì vì \(\left\{\begin{matrix} BH\perp AC\\ BH\perp AA'\end{matrix}\right.\) \(\Rightarrow BH\perp (ACC'A')\)
Khi đó \((BC',(ACC'A'))=\angle BC'H=30^0\)
\(\Rightarrow \sin 30=\frac{BH}{BC'}=\frac{1}{2}\Rightarrow BC'=\sqrt{3}a\) kéo theo \(BB'=\sqrt{BC'^2-B'C'^2}=\sqrt{2}a\)
\(\Rightarrow V_{ABC.A'B'C'}=BB'.S_{ABC}=\sqrt{2}a.\frac{\sqrt{3}a^2}{4}=\frac{\sqrt{6}a^3}{4}\)