Cho tam giác ABC vuông tại A có AH là đường cao. A/ C/m
1)tam giác ABC đồng dạng với tam giác HBA.
2) AB bình phương= BH x BC
3) AC bình phương = CH x BC
B/ Gọi AD là phân giác góc BAC, D thuộc BC. Cmr DB bình phương x CH =BH X DC bình phương
4) AB bình phương + AC bình phương= BC bình phương ( không dùng pytago)
5) AH bình phương = BH x BC
6) 1/AB bình phương 1/AC bình phương= 1/AH bình phương

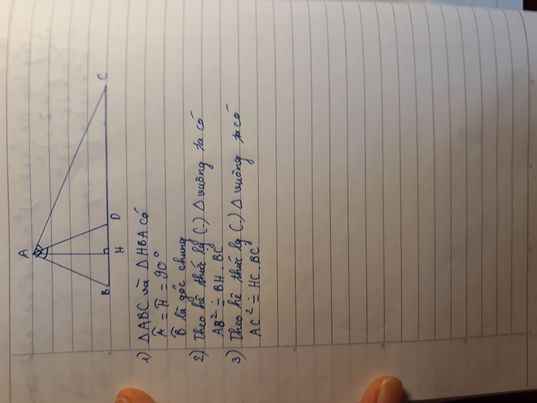
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
3: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔACH\(\sim\)ΔBCA
Suy ra: \(\dfrac{CA}{CB}=\dfrac{CH}{CA}\)
hay \(CA^2=CH\cdot CB\)