Tìm GTNN của biểu thức P=x2+xy+y2-2x-3y+2010 khi các số thực x,y thay đổi. Giá trị nhỏ nhất đó đạt được tại các giá trị nào của x và y.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 5 2021
\(x^2+y^2+xy=3\)
Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)
\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\)
Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)
mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)
=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1
maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 5 2021
Đặt \(P=x^2+y^2-xy\)
\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)
\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)
\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)
\(P_{min}=1\) khi \(x=y=1\)
\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow P\le9\)
\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)
CM
2 tháng 2 2019
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
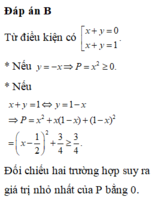
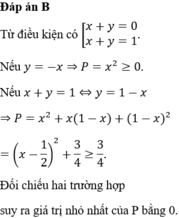
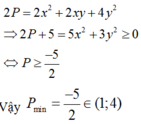
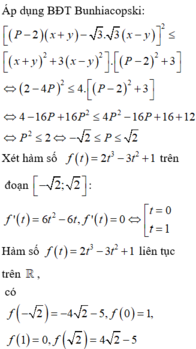
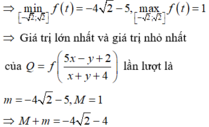
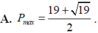
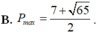
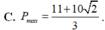
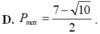
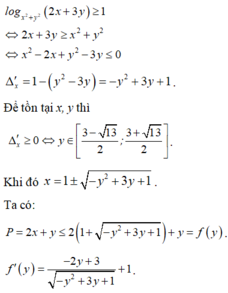
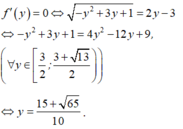
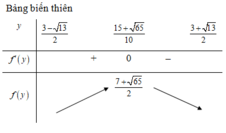
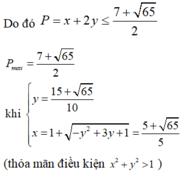
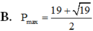
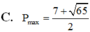
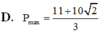
Ta có: P= \(x^2+xy+y^2-2x-3y+2010\)
\(\Leftrightarrow\) 4P= \(4\left(x^2+xy+y^2-2x-3y+2010\right)\)
= \(4x^2+4xy+4y^2-8x-12y+8040\)
= \(\left(4x^2+y^2+4+4xy-8x-8y\right)+3y^2-8y+8036\)
= \(\left(2x+y-2\right)^2+3y^2-8y+\dfrac{16}{3}-\dfrac{16}{3}+8036\)
= \(\left(2x+y-2\right)^2+3\left(y^2-\dfrac{8}{3}y+\dfrac{16}{9}\right)+\dfrac{24092}{3}\)
= \(\left(2x+y-2\right)^2+3\left(y-\dfrac{4}{3}\right)^2+\dfrac{24092}{3}\) \(\geq\) \(\dfrac{24092}{3}\)
\(\Rightarrow\) 4P \(\geq\) \(\dfrac{24092}{3}\) \(\Rightarrow\) P \(\geq\) \(\dfrac{6023}{3}\)
Dấu = xảy ra khi \(\begin{cases} (2x+y-2)^{2}=0\\ (y-\dfrac{4}{3})^{2}=0 \end{cases} \) \(\Leftrightarrow\) \(\begin{cases} 2x+y-2=0\\ y-\dfrac{4}{3}=0 \end{cases} \) \(\Leftrightarrow\) \(\begin{cases} 2x=-(y-2)\\ y=\dfrac{4}{3} \end{cases} \) \(\Leftrightarrow\) \(\begin{cases} 2x=-(\dfrac{4}{3}-2)\\ y=\dfrac{4}{3} \end{cases} \) \(\Leftrightarrow\) \(\begin{cases} x=\dfrac{1}{3}\\ y=\dfrac{4}{3} \end{cases} \)
Từ đó suy ra Min P= \(\dfrac{6023}{3}\) khi \(\begin{cases} x=\dfrac{1}{3}\\ y=\dfrac{4}{3} \end{cases} \)
Chúc bạn học tốt.