bài tập nâng cao ancol mình không biết giải các bạn gúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sgk toán 8 tập 1
Bài 74. Hai đường chéo của một hình thoi bằng 8cm8cm và 10cm10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) 6cm6cm; (B) √41cm41cm
(C) √164cm164cm (D) 9cm9cm ?
Bài giải:
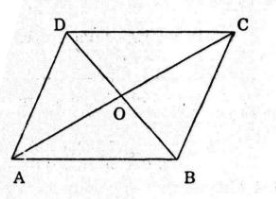
Xét bài toán tổng quát:
ABCDABCD là hình thoi, OO là giao điểm hai đường chéo.
Theo tính của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
Áp dụng định lí Pytago vào tam giác vuông ABOABO ta có:
AB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=√(12AC)2+(12BD)2=√42+52=√41cmAB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=(12AC)2+(12BD)2=42+52=41cm
Vậy (B) đúng.
Bài 79.
a) Một hình vuông có cạnh bằng 3cm3cm. Đường chéo của hình vuông đó bằng 6cm6cm, √18cm18cm, 5cm5cm hay 4cm4cm ?
b) Đường chéo của một hình vuông bằng 2dm2dm. Cạnh cảu hình vuông đó bằng: 1dm1dm,
32dm32dm, √2dm2dm hay 43dm43dm ?
Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là aa.
Ta có: a2=32+32=18a2=32+32=18
Suy ra a=√18a=18
Vậy đường chéo của hình vuông đó bằng √18cm18cm.
b) Gọi cạnh của hình vuông là aa.
Ta có a2+a2=22⇒2a2=4⇒a2=2⇒a=√2a2+a2=22⇒2a2=4⇒a2=2⇒a=2
Vậy cạnh của hình vuông đó bằng √2dm2dm.


bn lên mang tìm xem chứ mk thấy có rất nhiều tài liệu hay còn có đáp án nữa
http://tailieu.vn/doc/tuyen-tap-cac-dang-bai-tap-phuong-trinh-dai-so-lop-8-1716537.html
sao cái link lại nha

\(\text{Ta có:}\)
\(y^2=xz\Leftrightarrow\dfrac{x}{y}=\dfrac{y}{z}\left(1\right)\)
\(z^2=yt\Leftrightarrow\dfrac{x}{y}=\dfrac{t}{x}\left(2\right)\)
\(\text{Từ (1) và (2)}\Leftrightarrow\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{t}{x}\)
\(\Leftrightarrow\dfrac{x^3}{y^3}=\dfrac{y^3}{z^3}=\dfrac{t^3}{x^3}\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x^3}{y^3}=\dfrac{y^3}{z^3}=\dfrac{t^3}{x^3}=\dfrac{x^3+y^3+t^3}{y^3+z^3+x^3}\)
\(\Leftrightarrow\dfrac{x^3}{t^3}=\dfrac{y^3+z^3+x^3}{y^3+z^3+x^3}\left(đpcm\right)\)
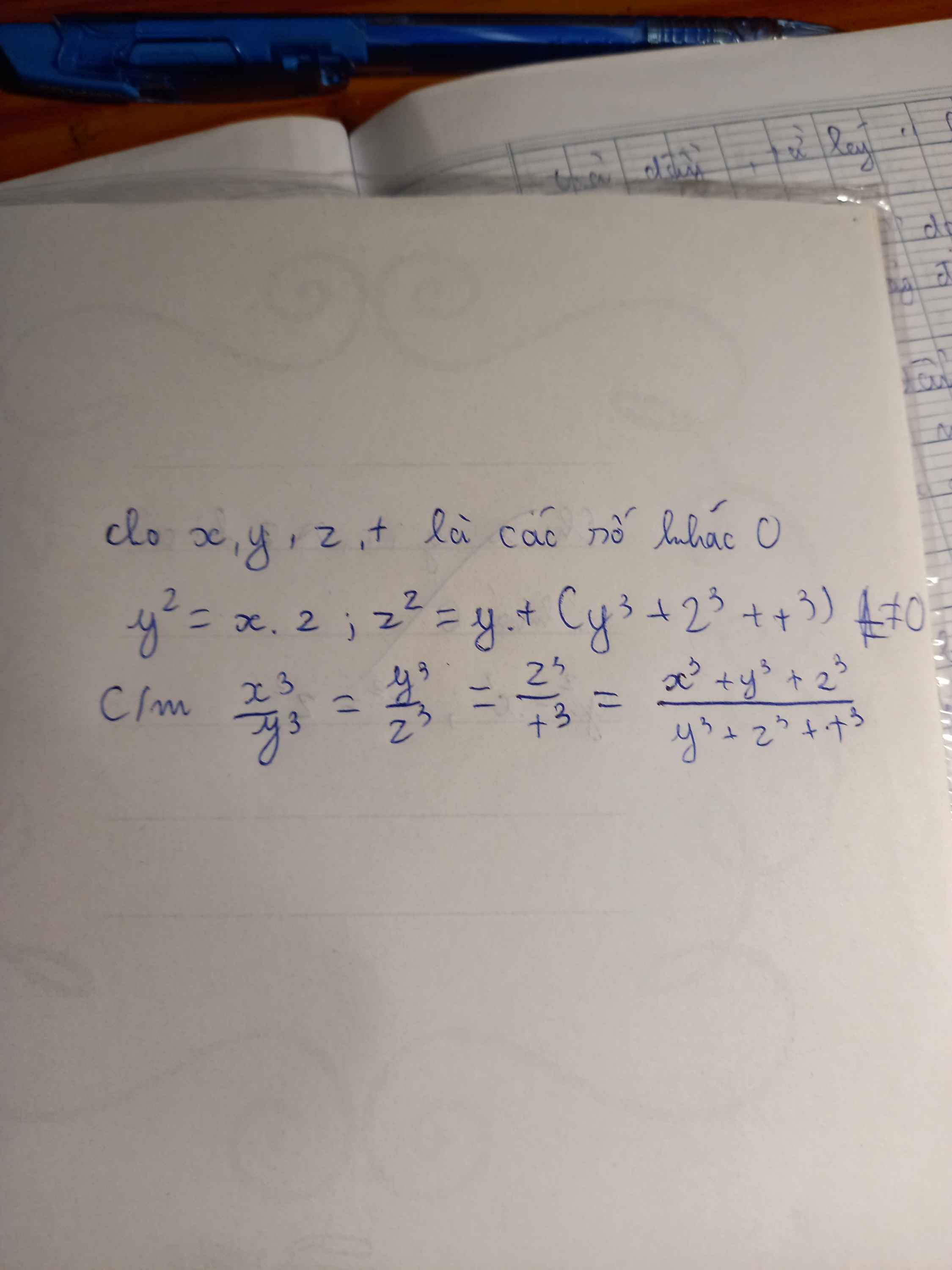
1.
a. nO2 = 0,3 (mol)
nCO2 = x (mol); nH2O = y (mol). Áp dụng bảo toàn khối lượng:
4,42 + 9,6 = 44x + 18y
Áp dụng bảo toàn oxi:
y-x + 0,3.2 = 2x + y (do là ankanol đơn nên nO = nankanol = nH2O - nCO2 = y - x), suy ra:
\(\left\{{}\begin{matrix}x=0,2\\y=0,29\end{matrix}\right.\)
Mtrung bình: \(\dfrac{4,42}{0,29-0,2}\) \(\simeq\) 49 suy ra: C2H5OH và C3H7OH
b. Giải hệ phương trình:
\(\left\{{}\begin{matrix}46x+60y=4,42\\x+y=0,09\end{matrix}\right.\)\(\rightarrow\) \(\left\{{}\begin{matrix}x=0,07\\t=0,02\end{matrix}\right.\)
%mC2H5OH = 72,85%; %mC3H7OH = 27,15%
2.
a. nCO2 = 1,05 (mol); nH2O = 1,2 (mol) \(\rightarrow\) nankanol = 1,2 - 1,05 = 0,15 (mol)
Đặt 23,8 g gồm: CaH2aO và CbH2b+2O2
mO trong ancol là: 23,8 - 1,05.12 - 1,2.2 = 8,8 (g) \(\rightarrow\) 0,55 (mol)
Ta có phương trình (bảo toàn oxi): x + 2y = 0,55 với x = nankenol và y = nankanol
Suy ra nankenol = 0,25 (mol)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(14a+16\right).0,25+\left(14b+34\right).0,15=23,8\\0,25a+0,15b=1,05\end{matrix}\right.\)\(\rightarrow\)\(\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
C3H5OH và C2H4(OH)2
%mankenol = 60,92%
%mankanol = 39,08%