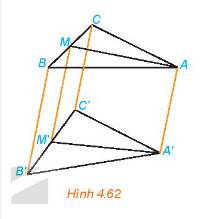
Trong mặt phẳng \(\left(\alpha\right)\) cho một tam giác ABC bất kì. Chứng minh rằng có thể xem tam giác ABC là hình chiếu song song của một tam giác đều nào đó ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
25 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
10 tháng 12 2017
Cho tam giác ABC bất kì nằm trong mặt phẳng (α). Gọi (β) là mặt phẳng qua BC và khác với (α). Trong (β) ta vẽ tam giác đều BCD. Vậy ta có thể xem tam giác ABC cho trước là hình chiếu song song của tam giác đều DBC theo phương chiếu DA lên mặt phẳng (α).
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Tham khảo hình vẽ:
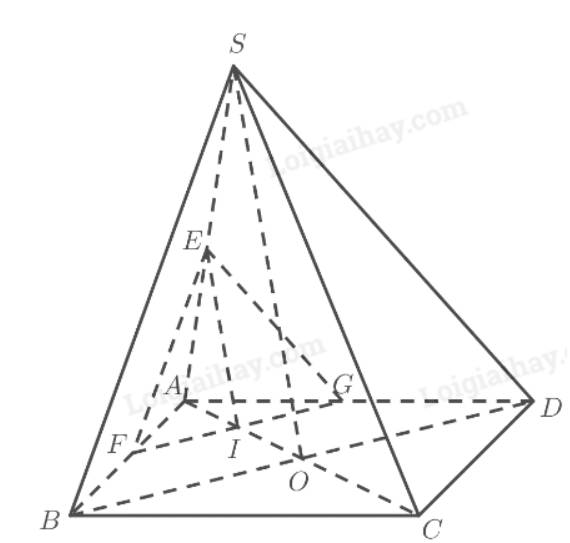
TH1: \(\left( \alpha \right)\) cắt đoạn \(AO\) tại \(I\).
Gọi \(E,F,G\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(SA,AB,AD\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = FG\\\left( {SBD} \right) \cap \left( {ABCD} \right) = B{\rm{D}}\end{array} \right\} \Rightarrow FG\parallel B{\rm{D}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{AG}}{{AD}} = \frac{{FG}}{{B{\rm{D}}}}\left( 1 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = EF\\\left( {SAB} \right) \cap \left( {SB{\rm{D}}} \right) = SB\end{array} \right\} \Rightarrow EF\parallel SB \Rightarrow \frac{{AF}}{{AB}} = \frac{{AE}}{{AS}} = \frac{{EF}}{{SB}}\left( 2 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SAD} \right) = EG\\\left( {SAD} \right) \cap \left( {SB{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow EG\parallel SD \Rightarrow \frac{{AG}}{{AD}} = \frac{{AE}}{{AS}} = \frac{{EG}}{{SD}}\left( 3 \right)\end{array}\)
Từ (1), (2) và (3) suy ra \(\frac{{EF}}{{SB}} = \frac{{EG}}{{S{\rm{D}}}} = \frac{{FG}}{{B{\rm{D}}}}\).
Tam giác \(SBD\) đều nên \(SB = SD = BD\).
Do đó \(EF = EG = FG\). Vậy tam giác \(EFG\) đều.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Tham khảo hình vẽ:
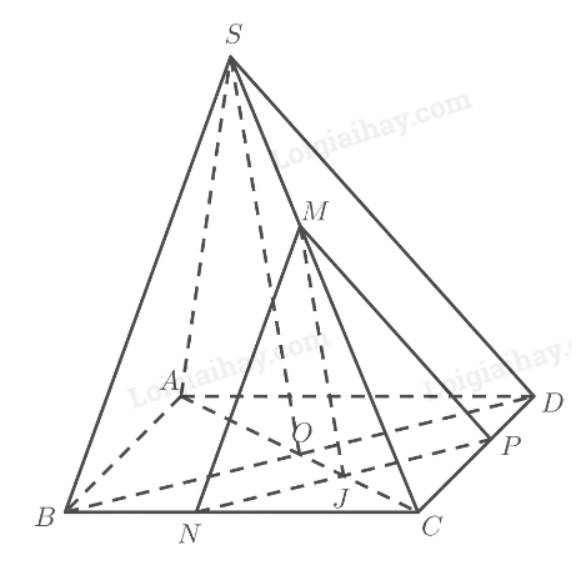
TH2: \(\left( \alpha \right)\) cắt đoạn \(CO\) tại \(J\).
Gọi \(M,N,P\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(SC,BC,C{\rm{D}}\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = NP\\\left( {SBD} \right) \cap \left( {ABCD} \right) = B{\rm{D}}\end{array} \right\} \Rightarrow NP\parallel B{\rm{D}} \Rightarrow \frac{{CN}}{{CB}} = \frac{{CP}}{{C{\rm{D}}}} = \frac{{NP}}{{B{\rm{D}}}}\left( 4 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SBC} \right) = MN\\\left( {SBC} \right) \cap \left( {SB{\rm{D}}} \right) = SB\end{array} \right\} \Rightarrow MN\parallel SB \Rightarrow \frac{{CM}}{{C{\rm{S}}}} = \frac{{CN}}{{CB}} = \frac{{MN}}{{SB}}\left( 5 \right)\\\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SBD} \right)\\\left( \alpha \right) \cap \left( {SCD} \right) = MP\\\left( {SCD} \right) \cap \left( {SB{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow MP\parallel SD \Rightarrow \frac{{C{\rm{M}}}}{{C{\rm{S}}}} = \frac{{CP}}{{C{\rm{D}}}} = \frac{{MP}}{{SD}}\left( 6 \right)\end{array}\)
Từ (4), (5) và (6) suy ra \(\frac{{MN}}{{SB}} = \frac{{MP}}{{S{\rm{D}}}} = \frac{{NP}}{{B{\rm{D}}}}\).
Tam giác \(SBD\) đều nên \(SB = SD = BD\).
Do đó \(MN = MP = NP\). Vậy tam giác \(MNP\) đều.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
MN là đường trung bình của tam giác ABC
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
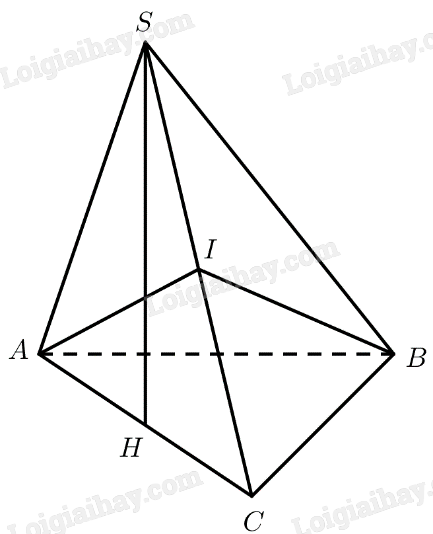
a) Gọi \(H\) là trung điểm của \(AC\)
\(SAC\) là tam giác đều \( \Rightarrow SH \bot AC\)
Mà \(\left( {SAC} \right) \bot \left( {ABC} \right)\)
\( \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot BC\)
Lại có \(AC \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SAC} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SAC} \right)\)
b) \(SAC\) là tam giác đều \( \Rightarrow AI \bot SC\)
\(BC \bot \left( {SAC} \right) \Rightarrow BC \bot AI\)
\(\left. \begin{array}{l} \Rightarrow AI \bot \left( {SBC} \right)\\AI \subset \left( {ABI} \right)\end{array} \right\} \Rightarrow \left( {ABI} \right) \bot \left( {SBC} \right)\)
22 tháng 9 2023
Tham khảo:
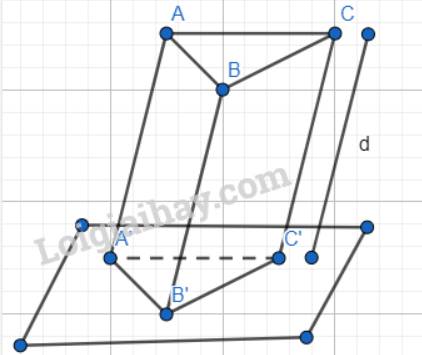
Nếu tam giác A′B′C′ là hình chiếu của tam giác ABC theo phương d thì tam giác ABC là hình chiếu của tam giác A′B′C′ vì tam giác ABC là tập hợp tất cả các hình chiếu của các điểm thuộc A'B'C' qua phép chiếu song song theo phương d.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
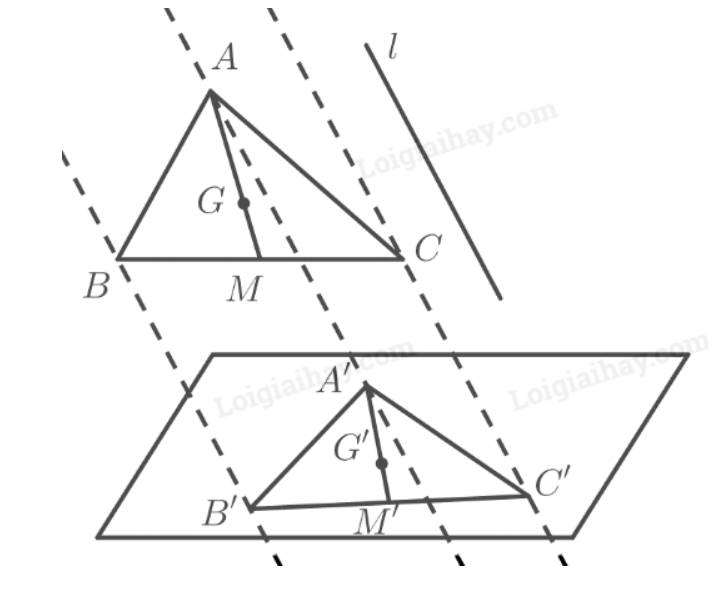
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Vì K là trung điểm BC nên B, K, C thẳng hàng theo thứ tự đó và BK = KC. Do vậy B', K', C' thẳng hàng theo thứ tự đó và B'K' = K'C', tức K' là trung điểm B'C'.
Vì G là trọng tâm tam giác ABC nên A, G, K thẳng hàng theo thứ tự đó và AG = 2GK. Do vậy A, G', K' thẳng hàng theo thứ tự đó và A'G' = 2G'K', tức G là trọng tâm tam giác A'B'C'.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
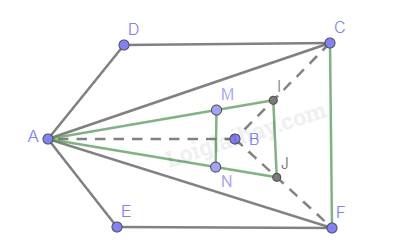
Gọi I,J lần lượt là trung điểm của BC, BF
Suy ra, IJ là đường trung bình của tam giác BCF.
Do đó, IJ // CF (1)
Tam giác AIJ có: \(\frac{{AM}}{{AI}} =\frac{{AN}}{{AJ}}= \frac{2}{3}\)
Suy ra, MN // IJ (theo Ta lét) (2)
Từ (1) và (2) suy ra MN // CF, mà CF nằm trong (ACF).
Suy ra MN // (ACF)
