TRÒ CHƠI TOÁN HỌC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
P(x) = x2 (7x – 5) – (28x5 – 20x4 – 12x3) : 4x2
= x2 . 7x – x2 . 5 – ( 28x5 : 4x2 – 20x4 : 4x2 – 12x3 : 4x2)
= 7x3 – 5x2 – (7x3 – 5x2 – 3x)
= 7x3 – 5x2 – 7x3 + 5x2 +3x
= (7x3 - 7x3 ) + (– 5x2 + 5x2 ) + 3x
= 0 +0 + 3x
=3x
Khi x = 5 thì P(5) = 3 . 5 =15
Vậy Vuông chỉ cần rút gọn biểu thức P(x), sau đó thay x = 5 vào P(x) đã rút gọn
CM
24 tháng 10 2017
Cách chơi: mỗi người đến lượt mình cố gắng bắn chìm các tàu của đối phương bằng một trong hai cách sau;
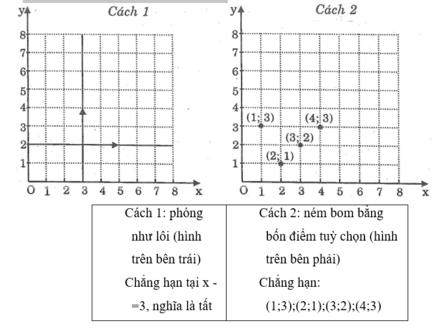
Sau mỗi lần băn của một người chơi, trọng tài có nhiệm vụ xá định và nói rõ đã trúng bao nhiêu điểm.
Ai bắn chìm hết các tàu của đối phương trước là thắng cuộc (một tàu coi là bị bắn chìm nếu bị trúng cả ba điểm)
29 tháng 5 2018
| a) Máy tính giúp em học làm toán, học vẽ. | Đ |
| b) Máy tính giúp em liên lạc với bạn bè. | Đ |
| c) Có nhiều loại máy tính khác nhau. | Đ |
| d) Em không thể chơi trò chơi trên máy tính | S |
QK
14 tháng 11 2015
Ta có
toán= nhạc = 2 thể thao = 4 làm thơ
toán/4=nhạc/4=thể thao/2=thơ
có 99 học trò
tính chất của dãy tỉ số bằng nhau
tất cả/ 4+4+2+1=99/11=9
Vậy lần lượt là 36
36
18
9
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 9 2024
Đây là toán nâng cao dạng ba tỉ số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em gải chi tiết dạng này như sau:
Giải:
Nếu không tính nhà bác học pytago thì tổng số học sinh là:
100 - 1 = 99 (học trò)
Số học trò học làm thơ bằng: \(\dfrac{1}{2}\) x \(\dfrac{1}{2}\) = \(\dfrac{1}{4}\) (số học trò học nhạc)
99 học trò ứng với phân số là:
1 + 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) = \(\dfrac{11}{4}\) (số học trò học nhạc)
Số học trò toán bằng số học trò học nhạc là: 99 : \(\dfrac{11}{4}\) = 36 (học trò)
Số học trò học toán là: 36 học trò.
GH
8 tháng 7 2023
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, k;
cin >> n >> k;
int ai[n];
for (int i = 0; i < n; i++) {
cin >> ai[i];
}
vector<int> pairs(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) continue;
if (ai[i] + ai[j] == k) {
pairs.push_back(make_pair(i, j));
}
}
}
sort(pairs.begin(), pairs.end());
int count = 0;
pairs.erase(pairs.begin(), pairs.end());
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (pairs[i].first == i && pairs[i].second == j) {
count++;
break;
}
}
if (count == n) {
break;
}
if (pairs[i].second == j) {
while (pairs[i].first != i) {
i++;
count++;
pairs.erase(pairs.begin() + i);
for (int j = 0; j < n; j++) {
if (ai[j] + ai[i] == k) {
pairs.push_back(make_pair(j, i+1));
break;
}
}
for (int j = 1;; j++) {
int count_n = 0, count_s = 0;
for (int i = j-1; i >= 0; i--) {
if (pairs[i].second == j) {
j++;
count_n++;
pairs.erase(pairs.begin() + i + 1);
pairs.er
GH
8 tháng 7 2023
#include<bits/stdc++.h>
using namespace std;
int main() {
int T, n;
cin>>T;
for(int t=0;t<T;t++){
int n,k,a,i;
cin>>n>>k;
int a[n];
for(int i=0;i<n;i++){
cin>>a[i];
}
int ans=0;
int c=0;
int sum=0;
int c0=0;
int c1=0;
int c2=0;
for(int i=0;i<n;i++){
sum+=a[i];
}
for(int i=0;i<n;i++){
if(sum<k && i!=0){
sum+=a[i]-1;
}
}
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
int sum=0;
for(int l=i;l<j;l++){
sum+=a[l];
}
if(sum==k){
c0=i;
c1=j;
}
}
}
printf("Case %d : %d - %d (c0,c1)\n",t+1,c*n+c0,c*n+c1);
++c;
}
return 0;
}
11 tháng 8 2023
Cách làm:
Số học sinh thích cả hai trò chơi = Số học sinh thích bóng rổ + Số học sinh thích bóng chuyền - Số học sinh thích ít nhất một trò chơi.
Theo đề bài, có 29 học sinh thích bóng rổ và 28 học sinh thích bóng chuyền. Vì mỗi học sinh phải chọn ít nhất 1 trò chơi, nên số học sinh thích ít nhất một trò chơi là tổng số học sinh lớp 5, tức là 42.
Áp dụng công thức trên, ta có:
Số học sinh thích cả hai trò chơi = 29 + 28 - 42 = 15.
Vậy có 15 học sinh thích cả hai trò chơi
Không có bảng thì không trò chơi.
Vs cách chơi của bạn thứ 2 , ta thấy ngay giá trị tuyệt đối của tổng cuối cx k nhỏ hơn :
\(19+20-1-1-...-1=30\)
------------- 9 số hạng -----
Như vậy , bạn hai luôn thắng.