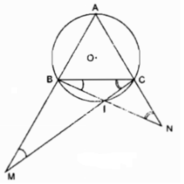
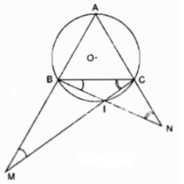
Cho đường tròn tâm O bán kính R. Lấy ba điểm A, B, C trên đường tròn đó sao cho \(AB=BC=CA\). Gọi I là điểm bất kì thuộc cung nhỏ BC (và I không trùng với B, C). Gọi M là giao điểm của CI với AB. Gọi N là giao điểm của BI với AC. Chứng minh :
a) \(\widehat{ANB}=\widehat{BCI}\)
b) \(\widehat{AMC}=\widehat{CBI}\)