Cho tam giac ABC can tai A.Tren can AB lay diem D,tren can AC lay diem E sao cho AD=AE.Goi M la giao diem cua BD va CD. Chung minh:
a) cac hinh chieu cua BD va CE tren BC bang nhau
b) BE=CD
c) tam giac BMD =tam giac CME
d) AM la tia p/g cua goc BAC
e) BE nho hon BC+DE:2
giup mk nha m. n can gap tick Cho

 10 K NHA !
10 K NHA !
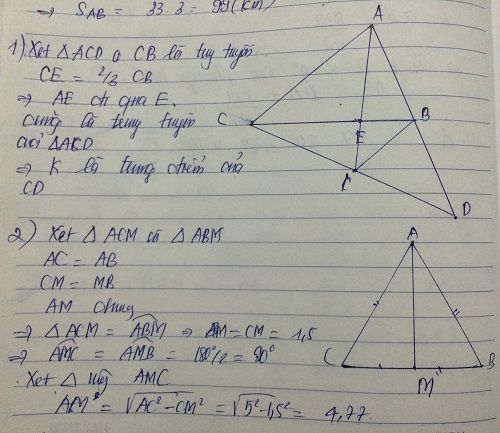
b) Xét hai tam giác ABE và ACD có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
AD = AE (gt)
Vậy: \(\Delta ABE=\Delta ACD\left(c-g-c\right)\)
Suy ra: BE = CD (hai cạnh tương ứng)
c) Ta có: \(\widehat{D_1}+\widehat{D_2}=180^o\)
\(\widehat{E_1}+\widehat{E_2}=180^o\)
Mà \(\widehat{D_1}=\widehat{E_1}\) (\(\Delta ABE=\Delta ACD\))
\(\Rightarrow\) \(\widehat{D_2}=\widehat{E_2}\)
Ta lại có: BD = AB - AD
CE = AC - AE
Mà AB = AC (do \(\Delta ABC\) cân tại A)
AD = AE (gt)
\(\Rightarrow\) BD = CE
Xét hai tam giác BDM và CEM có:
\(\widehat{ABE}=\widehat{ACD}\) (\(\Delta ABE=\Delta ACD\))
BD = CE (cmt)
\(\widehat{D_2}=\widehat{E_2}\) (cmt)
Vậy: \(\Delta BDM=\Delta CEM\left(g-c-g\right)\)
d) Xét hai tam giác ABM và ACM có:
AB = AC (do \(\Delta ABC\) cân tại A)
MB = MC (\(\Delta BDM=\Delta CEM\))
AM: cạnh chung
Vậy: \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AM là tia phân giác của \(\widehat{BAC}\) (đpcm).
Cho mk hỏi M là giao điểm của BE và CD hay của BD và CD vậy?