Một chiếc diểu ABCD có AB=BC=AD=DC. Biết AB = 12cm, \(\widehat{ADC}=40^0;\widehat{ABC}=90^0\) (h.25). Tính :
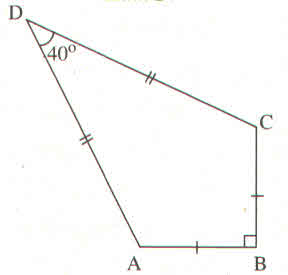
a) Chiều dài cạnh AD
b) Diện tích của chiếc diều
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)

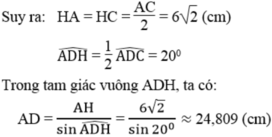
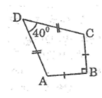
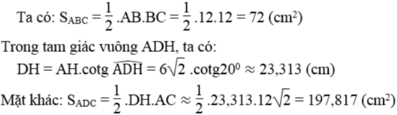
a) Nối AC và kẻ DH⊥ACDH⊥AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2=AB2+BC2=122+122=144+144=288AC2=AB2+BC2=122+122=144+144=288
Suy ra: AC=12√2(cm)AC=122(cm)
Ta có: tam giác ACD cân tại D
DH⊥ACDH⊥AC
Suy ra: HA=HC=AC2=6√2(cm)HA=HC=AC2=62(cm)
ˆADH=12ˆADC=20∘ADH^=12ADC^=20∘
Trong tam giác vuông ADH, ta có:
AD=AHsinˆADH=6√2sin20∘≈24,809(cm)AD=AHsinADH^=62sin20∘≈24,809(cm)
b) Ta có:
SABC=12.AB.BC=12.12.12=72SABC=12.AB.BC=12.12.12=72 (cm2)
Trong tam giác vuông ADH, ta có:
DH=AH.cotgˆADH=6√2.cotg20∘≈23,313(cm)DH=AH.cotgADH^=62.cotg20∘≈23,313(cm)
Mặt khác:
SADC=12.DH.AC≈12.23,313.12√2=197,817SADC=12.DH.AC≈12.23,313.122=197,817 (cm2)
Vậy Sdiều =SABC+SADC=72+197,817=269,817=SABC+SADC=72+197,817=269,817 (cm2)
a, nối AC rồi kẻ
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC:
Suy ra:
ta có:tam giác ABC cân tại D
Suy ra:
Trong tam giác vuông ADH, ta có
b, Ta có:
(cm2)
Trong tam giác vuông ADH, ta có:
Mặt khác
(cm2)
Vậy S (cm2)