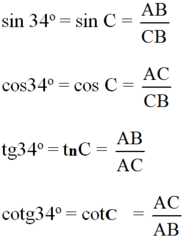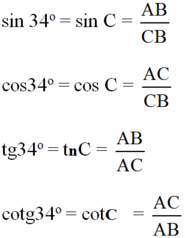Vẽ một tam giác vuông có một góc nhọn bằng \(40^0\) rồi viết các tỉ số lượng giác của góc \(40^0\) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
31 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
DP
2
HH
16 tháng 7 2020
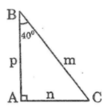
Vẽ tam giác ABC vuông tại A có \(\widehat{B}=90^o\)
Đặt AB = p ; AC = n ; BC = m
Ta có : \(sin40^o=sin\widehat{B}=\frac{AC}{BC}=\frac{n}{m}\)
\(cos40^o=cos\widehat{B}=\frac{AB}{BC}=\frac{p}{m}\)
\(tg40^o=tg \widehat{B } =\frac{AC}{AB}=\frac{n}{p}\)
\(cotg40^o=cotg \widehat{B} =\frac{AB}{AC}=\frac{p}{n}\)
LT
23 tháng 9 2021
Vẽ ∆ góc C = 40°
Góc A = 90°
→ Góc B = 50°
GIẢI
Tỉ số lượng giác của góc 40° là
Sin = AC/BC
Cos = AB/BC
Tg = AC/AB
Cot = AB/AC
SG
3
NL
24 tháng 4 2017
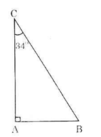
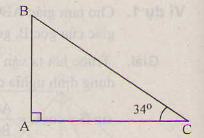
Vẽ tam giác ABC vuông tại A, góc C = 34°
Theo định nghĩa ta có:
24 tháng 4 2017
Hướng dẫn giải:
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.
PT
1
PT
1
B1
31 tháng 8 2017
Bài 10. Vẽ một tam giác vuông có một góc nhọn 34∘34∘ rồi viết các tỉ số lượng giác của góc 34∘34∘.
Hướng dẫn giải:
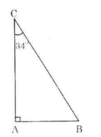
Vẽ tam giác ABC vuông tại A, ˆC=34∘C^=34∘
Theo định nghĩa ta có:
sin34∘=ABBCsin34∘=ABBC
cos34∘=ACBCcos34∘=ACBC
tg34∘=ABACtg34∘=ABAC
cotg34∘=ACABcotg34∘=ACAB.
Xem thêm tại: http://loigiaihay.com/bai-10-trang-76-sgk-toan-9-tap-1-c44a2814.html#ixzz4rLOPb3I0
TN
27 tháng 5 2016
a, giả sử tam giác ABC cân tại A có góc A=40
áp dụng định lý tổng 3 góc trong 1 tam giác ta có
góc A+góc B+góc C=180
hay 40+2.góc B=180
2.góc B=180-40
2.góc B=140
góc B=140:2=70 độ
Vậy 2 góc ở đáy =70 độ
b. giả sử tam giác ABC cân tại A có góc ở đáy =40 độ
Áp dụng định lý tổng 3 góc trong 1 tam giác ta có:
góc A+góc B+góc C=180
hay góc A+40+40=180
gocsA=180-80
góc A=100 độ
vậy góc ở đỉnh =100 độ
27 tháng 5 2016
a) Gọi ABC là tam giác cân đã cho và góc ở định =400
Ta có +2
=1800
2= 1800 -
= 1400
=> = 700
b) Ta có: +
+
=1800
mà =
=400
nên +2
=1800
+800 =1800
=400
17 tháng 10 2021
a: \(\widehat{B}=60^0\)
AB=8cm
\(AC=4\sqrt{3}\left(cm\right)\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)