Phần c ạ, em cần ngay bây giờ ạ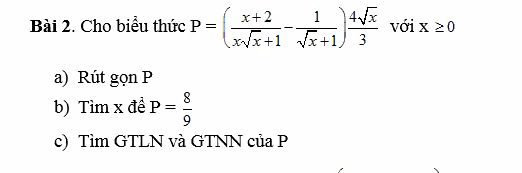
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
G
0

TM
0

NK
1



1 tháng 1 2022
\(a^3+b^3=2021c^3\\ \Leftrightarrow a^3+b^3+c^3=2022c^3⋮6\left(2022⋮6\right)\left(1\right)\)
Mặt khác: \(\left(a^3+b^3+c^3\right)-\left(a+b+c\right)=\left(a-1\right)a\left(a+1\right)+\left(b-1\right)b\left(b+1\right)+\left(c-1\right)c\left(c+1\right)\)
Có \(\left(a-1\right)a\left(a+1\right);\left(b-1\right)b\left(b+1\right);\left(c-1\right)c\left(c+1\right)\) là 3 cặp số nguyên liên tiếp nên chia hết cho 6
Do đó \(\left(a^3+b^3+c^3\right)-\left(a+b+c\right)⋮6\)
Kết hợp (1) ta được đpcm
 em cần gấp ngay bây giờ ạ mai em nộp bài rồi em cảm ơn ạ
em cần gấp ngay bây giờ ạ mai em nộp bài rồi em cảm ơn ạ


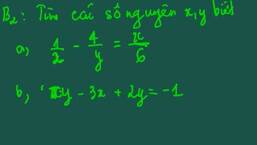


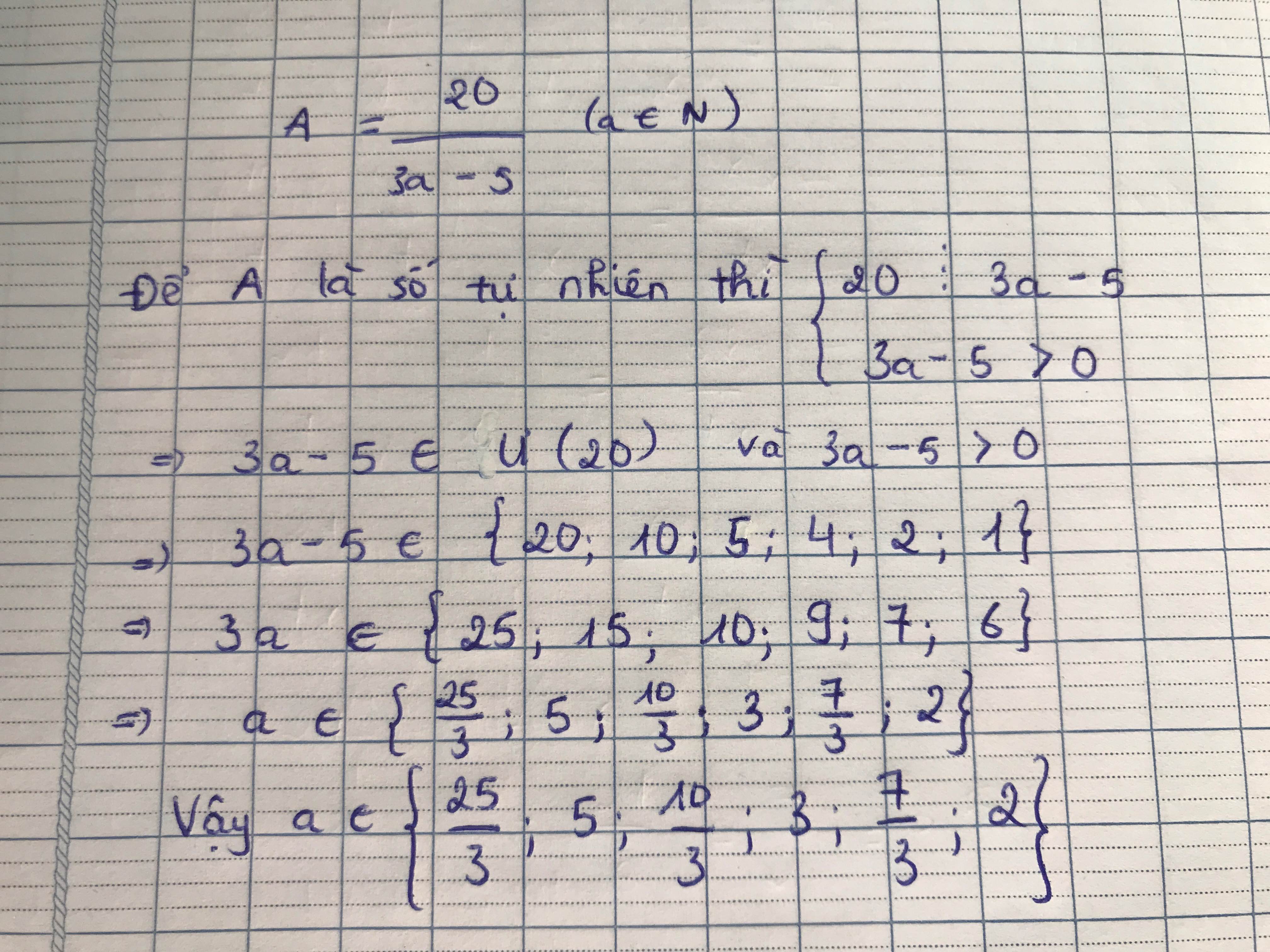
 giúp mình gấp! nhanh nha bạn, mình cần ngay bây giờ, các bạn làm dc bao nhiêu thì làm ạ, em cảm ơn rất nhiều!
giúp mình gấp! nhanh nha bạn, mình cần ngay bây giờ, các bạn làm dc bao nhiêu thì làm ạ, em cảm ơn rất nhiều!
\(P=\dfrac{4}{3}.\dfrac{\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{4}{3}\left(1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+1}\right)=\dfrac{4}{3}-\dfrac{4}{3}.\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+1}\le\dfrac{4}{3}\)
\(P_{max}=\dfrac{4}{3}\) khi \(x=1\)
Do \(\left\{{}\begin{matrix}\sqrt{x}\ge0\\x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow P\ge0\)
\(P_{min}=0\) khi \(x=0\)
a: Ta có: \(P=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right)\cdot\dfrac{4\sqrt{x}}{3}\)
\(=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\)
\(=\dfrac{4\sqrt{x}}{3x-3\sqrt{x}+3}\)