Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì công thức chu vi đường tròn là \(2\pi R\) với R là độ dài bán kính, trong đó \(\pi \) là số không thể tính chính xác được mà chỉ có thể lấy số gần đúng nên hai giá trị tính được là số gần đúng.
b)
Kết quả của An: \({S_1} = 2\pi R \approx 2.3,14.2 = 12,56\) cm:
Kết quả của Bình: \({S_2} = 2\pi R \approx 2.3,1.2 = 12,4\)cm.
Ta thấy \(\pi > 3,14 > 3,1 => 2.\pi. R > {S_1} > {S_2}\)
\( = > \left| {2\pi R - {S_1}} \right| < \left| {2\pi R - {S_2}} \right|\)
Nói cách khác, sai số tuyệt đối của \(S_1\) nhỏ hơn \(S_2\).
=> Kết quả của An chính xác hơn.
Thể tích hình cầu A là :
\(\dfrac{4}{3}x^3\pi\left(cm^3\right)\)
Thể tích hình cầu B là :
\(\dfrac{4}{3}\left(2x\right)^3\pi=\dfrac{4}{3}.8x^3\pi\left(cm^3\right)\)
Tỉ số thể tích hai hình cầu A và B là :
\(\dfrac{\dfrac{4}{3}x^3\pi}{\dfrac{4}{3}.8x^3\pi}=\dfrac{1}{8}\)
Vậy chọn (C)
\(S_{xq}=2\pi R.h=2\pi.5.7=70\pi\left(cm^2\right)\)
\(\Rightarrow B\)
-Chúc bạn học tốt-
a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:
Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5
c
m
3
thì trong các kết quả sau đây, kết quả nào là bán kính của nó (lấy 
)?
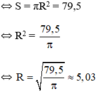
Bài 30 Nếu thể tích của một hình cầu là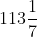
thì trong các kết quả sau đây, kết quả nào là bán kính của nó(lấy π= 22/7)?
(A) 2 cm (B) 3 cm (C) 5 cm (D) 6 cm ;
(E) Một kết quả khác.
Giải:
Từ công thức: V =
πR3 =>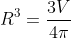 
Thay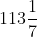
và π= 22/7 vào ta được
R3 = 27
Suy ra: R = 3
Vậy chọn B) 3cm