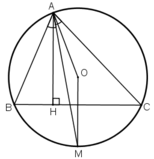
Cho tam giác ABC nội tiếp đường tròn (O) và tia phân giác của góc A cắt đường tròn tại M. Vẽ đường cao AH. Chứng minh rằng:
a) OM đi qua trung điểm của dây BC.
b) AM là tia phân giác của góc OAH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LS
Linh subi
17 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
CM
11 tháng 6 2019
Vì AM là tia phân giác
B
A
C
^
nên 
Suy ra M là điểm chính giữa của cung B C ⏜ , từ đó O M ⊥ B C và OM đi qua trung điểm của BC (định lí).
13 tháng 4 2023
a: góc ABI=1/2*sđ cung BI
góc ACI=1/2*sđ cung CI
=>sđ cung BI=sđ cung CI
=>BI=CI
mà OB=OC
nên OI là trung trực của BC
=>OI vuông góc BC tại M là trung điểm của BC
b: OI vuông góc BC
AH vuông góc CB
=>AH//OI
=>góc HAI=góc OIA=góc OAI
=>AI làphân giác của góc OAH
30 tháng 11 2023
a: Xét (O) có
\(\widehat{BAM}\) là góc nội tiếp chắn cung BM
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
\(\widehat{BAM}=\widehat{CAM}\)(AM là phân giác của góc BAC)
Do đó: \(sđ\stackrel\frown{BM}=sđ\stackrel\frown{CM}\)
=>MB=MC
=>M nằm trên đường trung trực của BC(1)
OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OM là đường trung trực của BC
=>OM\(\perp\)BC
b: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ADC}=\widehat{ABC}\)
Xét ΔACD vuông tại C và ΔAHB vuông tại H có
\(\widehat{ADC}=\widehat{ABH}\)
Do đó: ΔACD đồng dạng với ΔAHB
=>\(\widehat{CAD}=\widehat{HAB}\)
\(\widehat{BAH}+\widehat{HAM}=\widehat{BAM}\)
\(\widehat{CAD}+\widehat{MAD}=\widehat{CAD}\)
mà \(\widehat{BAH}=\widehat{CAD}\) và \(\widehat{BAM}=\widehat{CAD}\)
nên \(\widehat{HAM}=\widehat{MAD}\)
=>\(\widehat{IAM}=\widehat{DAM}\)
=>AM là phân giác của góc IAD
c: Xét (O) có
\(\widehat{IAM}\) là góc nội tiếp chắn cung IM
\(\widehat{DAM}\) là góc nội tiếp chắn cung DM
\(\widehat{IAM}=\widehat{DAM}\)
Do đó: \(sđ\stackrel\frown{IM}=sđ\stackrel\frown{DM}\)
=>IM=DM
=>M nằm trên đường trung trực của DI(3)
OI=OD
=>O nằm trên đường trung trực của DI(4)
Từ (3) và (4) suy ra OM là đường trung trực của DI
=>OM\(\perp\)DI
mà OM\(\perp\)BC
nên DI//BC