Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABI=1/2*sđ cung BI
góc ACI=1/2*sđ cung CI
=>sđ cung BI=sđ cung CI
=>BI=CI
mà OB=OC
nên OI là trung trực của BC
=>OI vuông góc BC tại M là trung điểm của BC
b: OI vuông góc BC
AH vuông góc CB
=>AH//OI
=>góc HAI=góc OIA=góc OAI
=>AI làphân giác của góc OAH

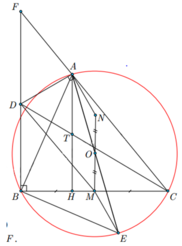
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
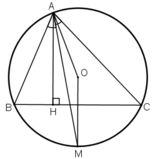


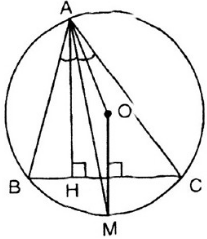
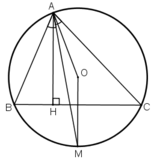

Vì AM là tia phân giác B A C ^ nên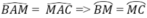
Suy ra M là điểm chính giữa của cung B C ⏜ , từ đó O M ⊥ B C và OM đi qua trung điểm của BC (định lí).