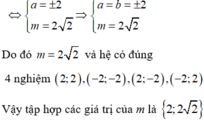- tìm giá trị của tham số m thoả các điều kiện sau

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình hoành độ giao điểm:
\(-2x^2=x-m\Leftrightarrow2x^2+x-m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=1+8m>0\Rightarrow m>-\dfrac{1}{8}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{1}{2}\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Leftrightarrow-\dfrac{1}{2}=-\dfrac{m}{2}\)
\(\Rightarrow m=1\) (thỏa mãn)

\(x^2+\left(4m+1\right)x+2\left(m-4\right)=0\)
\(\Delta=\left(4m+1\right)^2-4\cdot1\cdot2\left(m-4\right)=16m^2+8m+1-8m+32=16m^2+33\ge33>0\forall m\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-\left(4m+1\right)+\sqrt{16m^2+33}}{2}\\x_2=\dfrac{-\left(4m+1\right)-\sqrt{16m^2+33}}{2}\end{matrix}\right.\)
Mà: \(x_2-x_1=17\)
\(\Leftrightarrow\dfrac{-\left(4m+1\right)-\sqrt{16m^2+33}}{2}-\dfrac{-\left(4m+1\right)+\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\dfrac{-\left(4m+1\right)-\sqrt{16m^2+33}+\left(4m+1\right)-\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\dfrac{-2\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\sqrt{16m^2+33}=-17< 0\)
Vậy không có m thỏa mãn

m là số tự nhiên nên ta chọn m nhỏ nhất là 0.
Khi đó m . 7920 = 0 . 7920 = 0 = 02
Vậy GTNN của m là 0 thỏa mãn điều kiện

\(\left\{{}\begin{matrix}mx-y=5\left(1\right)\\2x+3my=7\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}3m^2x-3my=3m5\\2x+3my=7\end{matrix}\right.\)
=> \(x\left(3m^2+2\right)=15m+7\)<=> \(x=\dfrac{15m+7}{3m^2+2}\)
Thay (1) : \(y=mx-5=\dfrac{15m^2+7m}{3m^2+2}-5=\dfrac{7m-10}{3m^2+2}\)
Ta có : \(\left\{{}\begin{matrix}x>0\\y< 0\end{matrix}\right.< =>\left\{{}\begin{matrix}15m+7>0\\7m-20< 0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}m>-\dfrac{7}{15}\\m< \dfrac{10}{7}\end{matrix}\right.\)
=> m\(\in\left(-\dfrac{7}{15};\dfrac{10}{7}\right)\)

Đặt z=x+yi ta có hệ đều kiện:
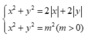
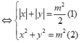
Ta có (1) là tập hợp các cạnh của hình vuông ABCD có tâm là gốc toạ độ độ dài cạnh bằng a = m 2 2 ; là đường tròn (C) có tâm là gốc toạ độ O bán kính bằng R = m.
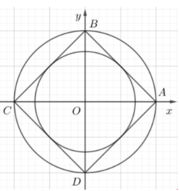
Để có đúng 8 số phức thoả mãn thì (C) phải nằm giữa đường tròn ngoại tiếp và đường tròn nội tiếp hình vuông 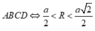
![]()
Chọn đáp án D.