Cho tam giác ABC đều cạnh a. Chọn hệ tọa độ \(\left(O;\overrightarrow{i};\overrightarrow{j}\right)\), trong đó O là trung điểm của cạnh BC, \(\overrightarrow{i}\)cùng hướng với \(\overrightarrow{OC}\), \(\overrightarrow{j}\) cùng hướng với \(\overrightarrow{OA}\) :
a) Tính tọa độ của các đỉnh của tam giác ABC
b) Tìm tọa độ trung điểm E của AC
c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC

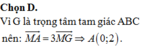



TenAnh1 TenAnh1 A = (-4.3, -5.94) A = (-4.3, -5.94) A = (-4.3, -5.94) B = (11.06, -5.94) B = (11.06, -5.94) B = (11.06, -5.94) C = (-4.34, -5.84) C = (-4.34, -5.84) C = (-4.34, -5.84) D = (11.02, -5.84) D = (11.02, -5.84) D = (11.02, -5.84)
\(OB=OC=\dfrac{a}{2}\).
\(OA=\sqrt{BC^2-OC^2}=\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{3}}{2}\).
Vậy \(C\left(\dfrac{a}{2};0\right);B\left(-\dfrac{a}{2};0\right);A\left(0;\dfrac{a\sqrt{3}}{2}\right)\).
b) \(x_E=\dfrac{x_A+x_C}{2}=\dfrac{a}{4}\); \(y_E=\dfrac{y_A+y_C}{2}=\dfrac{a\sqrt{3}}{4}\).
Vậy \(E\left(\dfrac{a}{4};\dfrac{a\sqrt{3}}{4}\right)\).
c)Do tam giác ABC đều cạnh a nên tâm đường tròn ngoại tiếp chính là trọng tâm tam giác ABC.
\(x_I=\dfrac{x_A+x_B+x_C}{3}=0\);
\(y_I=\dfrac{x_A+y_B+y_C}{3}=\dfrac{a\sqrt{3}}{6}\).
Vậy \(I\left(0;\dfrac{a\sqrt{3}}{6}\right)\).