Một vật rơi tự do theo phương trình \(s=\dfrac{1}{2}gt^2\), trong đó \(g\approx9,8m\)/\(s^2\) là gia tốc trọng trường
a) Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ \(t\left(t=5s\right)\) đến \(t+\Delta t\), trong các trường hợp \(\Delta t=0,1s;\Delta t=0,05s;\Delta t=0,001s\)
b) Tìm vận tốc tức thời của chuyển động tại thời điểm \(t=5s\)


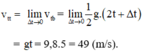
a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t + ∆t là
vtb = =
=  =
=  g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
Với t = 5 và
+) ∆t = 0.1 thì vtb ≈ 4,9. (10 + 0,1) ≈ 49,49 m/s;
+) ∆t = 0,05 thì vtb ≈ 4,9. (10 + 0,05) ≈ 49,245 m/s;
+) ∆t = 0,001 thì vtb ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s.
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5s tương ứng với ∆t = 0 nên v ≈ 4,9 . 10 = 49 m/s.