Dựa vào đồ thị hàm số \(y=\cos x\), tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
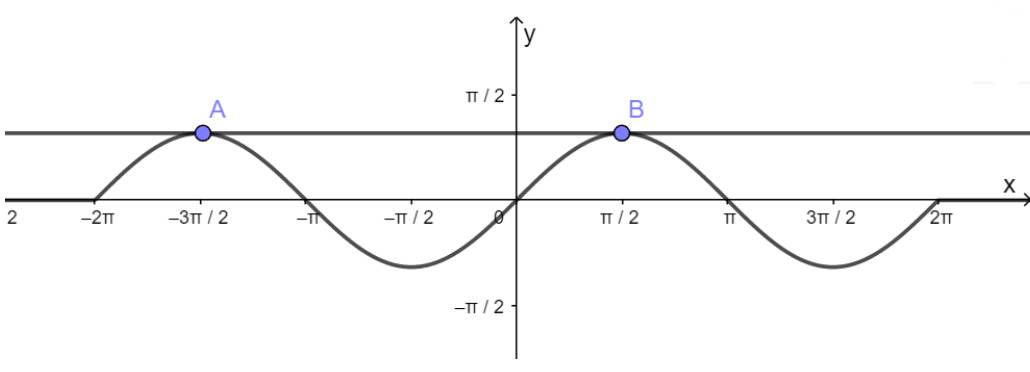
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
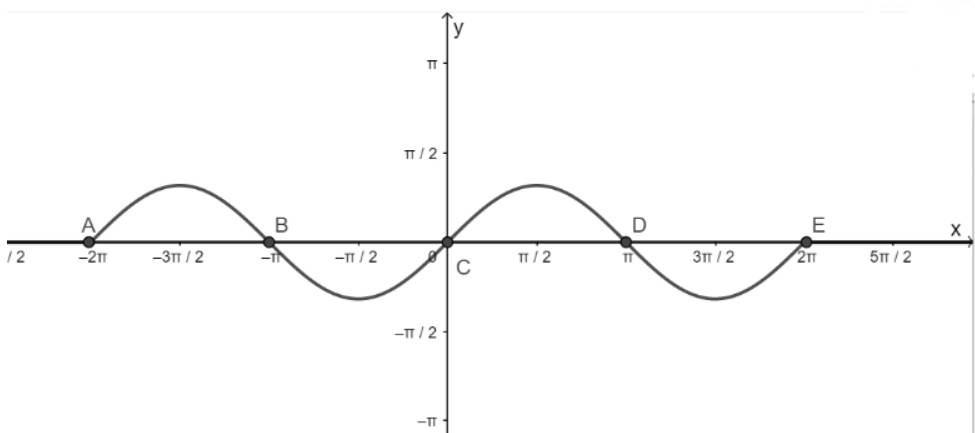
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
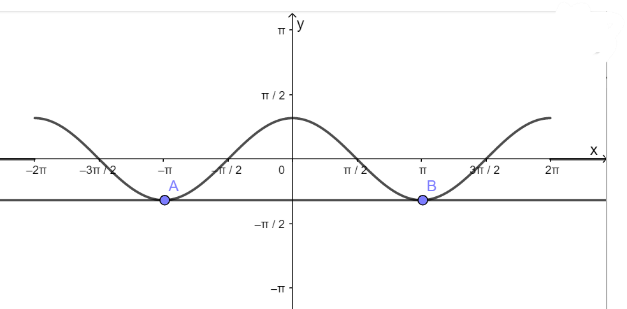
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
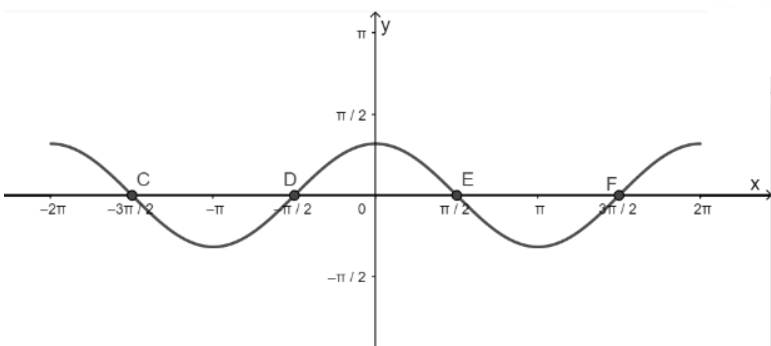
a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)
PT
Vẽ đồ thị của hàm số y = f(x) = 1,5x. Bằng đồ thị, hãy tìm: Các giá trị của x khi y dương; khi y âm.
1
CM
10 tháng 10 2018
Vẽ đồ thị hàm số:
Vẽ hệ trục tọa độ Oxy
Với x= 2 thì y = 1,5. 2 = 3 ta được điểm A(2; 3)
Vẽ đường thẳng đi qua O, A ta được đồ thị hàm số y = f(x) = 1,5x
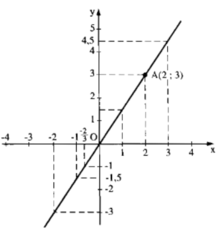
- Khi y dương: y > 0 ⇒ 1,5x > 0 ⇒ x > 0
- Khi y âm: y < 0 ⇒ 1,5x < 0 ⇒ x < 0
PT
1
CM
3 tháng 2 2017
Các giá trị của x khi y dương, khi y âm.
* Từ đồ thị đã cho ta thấy khi y dương và đồ thị nằm ở góc phần tư thứ II, các điểm thuộc đồ thị có hoành độ âm (nhỏ hơn không).
Vậy khi y dương thì x có giá trị âm.
* Tương tự khi y âm thì đồ thị nằm ở góc phần tư thứ IV, các điểm thuộc đồ thị có hoành độ dương.
Vậy khi y âm thì x có giá trị dương.
10 tháng 1 2022
a: f(4)=-2
f(-4)=2
f(6)=-3
f(0)=0
b: y=-3 thì -0,5x=-3
hay x=6
y=0 thì -0,5x=0
hay x=0
y=3,5 thì -0,5x=3,5
hay x=-7
c: Để y dương thì -0,5x>0
hay x<0
Để y âm thì -0,5x<0
hay y>0
B
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Đồ thị hàm số y = cosx và y = sinx giao nhau tại điểm x thoả mãn
\(cosx = sinx \Leftrightarrow cosx = cos\left( {\frac{\pi }{2} - x} \right)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} - x + k2\pi \\x = - \frac{\pi }{2} + x + k2\pi \end{array} \right. \Leftrightarrow x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}.\)
Vậy \(x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}.\)
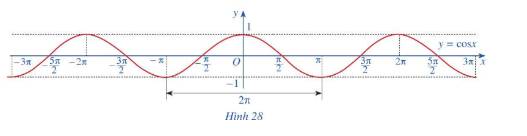
Dựa vào đồ thị hàm số y = cosx, để làm số nhận giá trị âm thì:
x∈(−3π2;−π2);(π2;3π2)...⇒x∈(π2+k2π;3π2+k2π),k∈Zx∈(−3π2;−π2);(π2;3π2)...⇒x∈(π2+k2π;3π2+k2π),k∈Z