Cho 3 mặt phẳng \(\left(\alpha\right),\left(\beta\right),\left(\gamma\right)\). Mệnh đề nào sau đây đúng ?
a) Nếu \(\left(\alpha\right)\perp\left(\beta\right)\) và \(\left(\alpha\right)\backslash\backslash\left(\gamma\right)\) thì \(\left(\beta\right)\perp\left(\gamma\right)\)
b) Nếu \(\left(\alpha\right)\perp\left(\beta\right)\) và \(\left(\alpha\right)\perp\left(\gamma\right)\) thì \(\left(\beta\right)\backslash\backslash\left(\gamma\right)\)

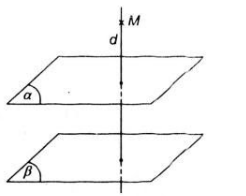

a) Đúng, vì nếu gọi m là đường thẳng vuông góc với β và n là đường thẳng vuông góc với hai mặt phẳng song song α, γ thì góc (m, n) = (β, α) = (β, γ), mà β ⊥ α nên β ⊥ γ.
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.