Cho \(\Delta MNP\) có I nằm giữa MP
CMR: \(NI< \dfrac{MN+NP+PM}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e) Gọi O là giao điểm của IP và HK. Chứng minh \(\widehat{MON}\) = 180o + \(\widehat{PMO}+\widehat{PNO}+\widehat{HIK}\)


a/ Xét tam giác MNI và tam giác MPI có:
\(\hept{\begin{cases}MN=MP\left(gt\right)\\NI=IP\left(gt\right)\\MI:canhchung\end{cases}}\)
suy ra tam giác MNI = tam giác MPI
Vậy : ....... ( đpcm )
Nhớ k cho mình nhé! Thank you!!!

a: Xét ΔPAN có
PM vừa là đường cao, vừa là trung tuyến
=>ΔPAN cân tại P
b: \(PM=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPAN có
NB,PM là trung tuyến
NB cắt PM tại G
=>G là trọng tâm
GP=2/3*3=2cm
c: CI là trung trực của MP
=>I là trung điểm của MP và CI vuông góc MP tại I
Xét ΔMPN có
I là trung điểm của PM
IC//MN
=>C là trung điểm của PN
=>PM,NB,AC đồng quy

Xét `\Delta PMI` và `\Delta PHI`:
`\text {PH = PM (gt)}`
$\widehat {MPI} = \widehat {HPI} (\text {tia phân giác} \widehat {MPN}$
`\text { PI chung}`
`=> \Delta PMI = \Delta PHI (c-g-c)`
`-> \text {IM = IH (2 cạnh tương ứng)}`
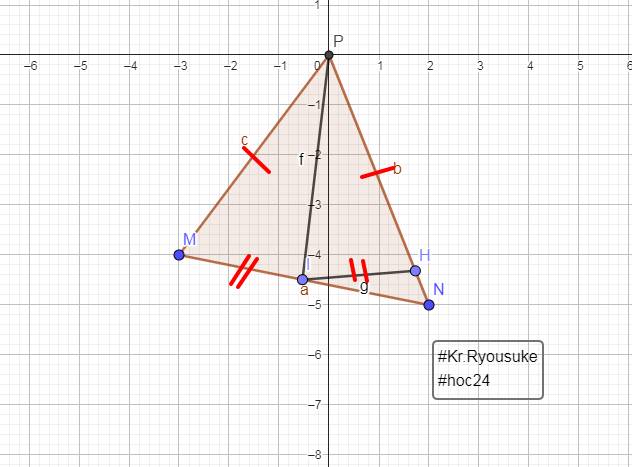
Ta có hình vẽ:
Trong tam giác MIN có:
MI + MN > NI => \(\dfrac{MI+MN}{2}\)> NI / 2 (1)
Trong tam giác PIN có:
PI + PN > NI => \(\dfrac{PI+PN}{2}\)> NI/2 (2)
Từ (1),(2)
=> (MI + MN + PI + PN) / 2 = 2.NI/2
hay \(\dfrac{MN+NP+PN}{2}\)> NI