Cho tam giác ABC, biết \(A\left(1;4\right),B\left(3;-1\right),C\left(6;2\right)\)
a) Lập phương trình tổng quát của các đường thẳng AB, BC, CA
b) Lập phương trình tổng quát của đường cao AH và trung tuyến AM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) TA CÓ 1/22-1=(1/2-1)x(1/2+1)=-1/2x3/2
1/32-1=(1/3-1)x(1/3+1)=-2/3X4/3..............1/992-1=(1/99-1)(1/99+1)=-98/99x100/99;1/1002-1=(1/100-1)x(1/100+1)=-99/100x101/100
ta có A=-(1/2x2/3x.....98/99x99/100)x(3/2x4/3x......x100/99x101/100)=-1/100x101/2=-101/50<-1/2
TA CÓ 1/22-1=(1/2-1)X(1/2+1)=-1/2X3/2 ;1/32-1=(1/3-1)X(1/3+1)=-2/3X4/3.....................
1/992-1=(1/99-1)X(1/99+1)=-98/99X100/99 ;1/1002-1=(1/100-1)X(1/100+1)=99/100X101/100
VẬY A=-(1/2X2/3X.......X98/99X99/100)X(3/2X4/3X....X100/99X101/100)=-101/50<-1/2

2) \(A=\left(\frac{1}{2^2}-1\right).\left(\frac{1}{3^2}-1\right).\left(\frac{1}{4^2}-1\right)...\left(\frac{1}{100^2}-1\right)\)
\(A=\frac{-3}{2^2}.\frac{-8}{3^2}.\frac{-15}{4^2}...\frac{-9999}{100^2}\)
\(A=-\left(\frac{3}{2^2}.\frac{8}{3^2}.\frac{15}{4^2}...\frac{9999}{100^2}\right)\) (vì có 99 thừa số âm nên kết quả là âm)
\(A=-\left(\frac{1.3}{2.2}.\frac{2.4}{3.3.}.\frac{3.5}{4.4}...\frac{99.101}{100.100}\right)\)
\(A=-\left(\frac{1.2.3...99}{2.3.4...100}.\frac{3.4.5...101}{2.3.4...100}\right)\)
\(A=-\left(\frac{1}{100}.\frac{101}{2}\right)\)
\(A=-\frac{101}{200}< -\frac{100}{200}=-\frac{1}{2}\)
Trả lời câu nào cũng được nha mấy bạn! Help me, please!!!!!!! ![]()
![]()

Câu hỏi của Phạm Thị Hường - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài làm ở link này nhé!

\(\overrightarrow{AB}\left(2;2\right);\overrightarrow{AC}\left(2;-2\right)\)
\(\overrightarrow{AB}.\overrightarrow{AC}=2.2+2.\left(-2\right)=0\) nên \(AB\perp AC\). (1)
\(AB=\sqrt{2^2+2^2}=2\sqrt{2}\).
\(AC=\sqrt{2^2+\left(-2\right)^2}=2\sqrt{2}\)
Vì vậy AB = AC. (2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại A.

Lời giải:
Ta có: $S_{ABC}=\frac{h_a.a}{2}$
$S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$ theo công thức Heron.
$\Rightarrow \frac{h_a.a}{2}=\sqrt{p(p-a)(p-b)(p-c)}$
$\Leftrightarrow \frac{a\sqrt{p(p-a)}}{2}=\sqrt{p(p-a)(p-b)(p-c)}$
$\Leftrightarrow \frac{a}{2}=\sqrt{(p-b)(p-c)}$
$\Rightarrow \frac{a}{2}=\frac{1}{2}\sqrt{(a+c-b)(a+b-c)}$
$\Rightarrow a^2=(a+c-b)(a+b-c)$$\Leftrightarrow a^2=a^2-(b-c)^2\Rightarrow (b-c)^2=0$
$\Rightarrow b=c$ hay $ABC$ là tam giác cân.

a=b=c=1 suy ra Tam giác ABC là tam giác đều vì có độ dài 3 canh = nhau .

Bài 1:
\(\Leftrightarrow n^2-1+2⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;2\right\}\)
hay \(n\in\left\{0;1\right\}\)
Bài 4:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
\(\widehat{A}\) chung
Do đó: ΔAHB\(\sim\)ΔAKC
Suy ra: AH/AK=AB/AC
hay AH/AB=AK/AC
Xét ΔAHK và ΔABC có
AH/AB=AK/AC
\(\widehat{HAK}\) chung
Do đó: ΔAHK\(\sim\)ΔABC
Suy ra: \(\widehat{AHK}=\widehat{ABC}\)
a) Ta có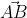 = (2; -5). Gọi M(x; y) là 1 điểm nằm trên đường thẳng AB thì AM = (x - 1; y - 4). Ba điểm A, B, M thẳng hàng nên hai vec tơ
= (2; -5). Gọi M(x; y) là 1 điểm nằm trên đường thẳng AB thì AM = (x - 1; y - 4). Ba điểm A, B, M thẳng hàng nên hai vec tơ 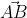 và
và 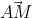 cùng phương, cho ta:
cùng phương, cho ta:
Đó chính là phương trình đường thẳng AB.
Tương tự ta có phương trình đường thẳng BC: x - y -4 = 0
phương trình đường thẳng CA: 2x + 5y -22 = 0
b) Đường cao AH là đường thẳng đi qua A(1; 4) và vuông góc với BC.
AH : 3(x - 1) + 3(y -4) = 0
3x + 3y - 15 = 0
=> x + y - 5 = 0
Gọi M là trung điểm BC ta có M \(\left(\dfrac{9}{2};\dfrac{1}{2}\right)\)
Trung tuyến AM là đường thẳng đi qua hai điểm A, M. Theo các viết phương trình đường thẳng đi qua hai điểm trong câu a) ta viết được:
AM : x + y - 5 = 0
mạnh nhể, làm cả toán 10