Cho lục giác đều ABCDEF có tâm O. Số các vectơ khác \(\overrightarrow{0}\) cùng phương với \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh của lục giác bằng bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
18 tháng 5 2017
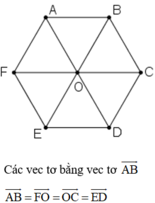
Các véc tơ bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là: \(\overrightarrow{FO};\overrightarrow{AB};\overrightarrow{ED}\).
Vậy có 3 véc tơ.
CM
22 tháng 12 2018
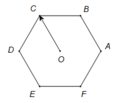
Các vecto cùng phương O C → với có điểm đầu và điểm cuối là các đỉnh của lục giác
: .
Chọn C.
CM
12 tháng 6 2019
Chọn C.
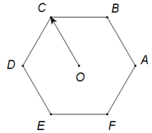
Các vecto cùng phương với 
có điểm đầu và điểm cuối là các đỉnh của lục giác : 
BT
18 tháng 5 2017
Các véc tơ bằng véc tơ \(\overrightarrow{AB}\) là:
\(\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\).
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Chắc là lục giác đều?
Các vecto bằng \(\overrightarrow{AB}\) là \(\overrightarrow{FO};\overrightarrow{OC};\overrightarrow{ED}\)
AH
Akai Haruma
Giáo viên
19 tháng 10 2018
Lời giải:
Các vecto khác vecto $0$ mà cùng phương với \(\overrightarrow{OC}\) có điểm đầu điểm cuối là đỉnh lúc giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FC};\overrightarrow{CF}; \overrightarrow{ED};\overrightarrow{DE}\)
Đáp án B
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
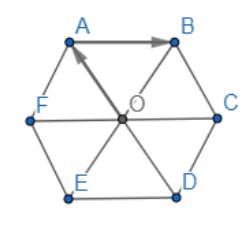
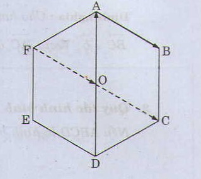
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)
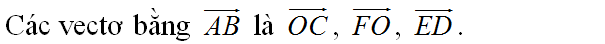
8
Số các véc tơ khác \(\overrightarrow{0}\) bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FO};\overrightarrow{OF};\overrightarrow{ED};\overrightarrow{DE};\overrightarrow{FC};\overrightarrow{CF}\).
Có 8 véc tơ.