Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Như vậy tích của phân số đó với các phân số: 11/5; 21/11; 28/25 đều là số tự nhiên.
=> Tử số của phân số đó phải chia hết cho 5; 11 và 25
Mấu số của phân số đó phải chia hết cho 11, 21 và 28
BSCNN của 5, 11 và 25 là: 11x25=275
BSCNN của 11, 21 và 28 là: 7x3x4x11=924
=> phân số cần tìm là: 275/924
Gọi a là số nguyên dương cần tìm
Để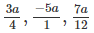 
là những số nguyên thì a phải chia hết cho 4, cho 11, cho 12; a là số nguyên dương nhỏ nhất nên a là BCNN(4,11,12) = 132.
a. Mẫu số chung nhỏ nhất là 24
b. \(\dfrac{5}{7}\)
c. \(\dfrac{3}{4}\)
d. \(\dfrac{9}{12}\) và giữ nguyên phân số còn lại
e. \(\dfrac{3}{6};\dfrac{4}{6};\dfrac{5}{6}\)
g. \(\dfrac{9}{12};\dfrac{4}{12};\dfrac{2}{12}\)
h. \(\dfrac{15}{60};\dfrac{20}{60};\dfrac{12}{60}\)
i. \(\dfrac{10}{1}\)
gọi a là số nguyên dương cần tìm
để 3a/4,-5a/11,7a/12 là những số nguyên thì a phải chia hết cho 4,cho11,cho12;a là số nguyên dương nhỏ nhất nên a là BCNN(4,11,12)=132
Gọi phân số tối giản cần tìm là \(\dfrac{a}{b}\)
Ta có:\(\dfrac{a}{b}\):\(\dfrac{5}{11}\)=\(\dfrac{11a}{5b}\)
\(\dfrac{a}{b}\):\(\dfrac{11}{21}\)\(\dfrac{21a}{11b}\)
\(\dfrac{a}{b}\):\(\dfrac{25}{28}\)=\(\dfrac{28a}{25b}\)
Vì cả 3 thương trên là số tự nhiên nên a chia hết cho 5,11,25\(\)\(\Rightarrow\)a\(\in\)BCNN(5;11;25)\(\Rightarrow\)a=275
Do đó b\(\in\)ƯCLN(11,21,28)=1
Vậy phân số tối giản cần tìm là \(\dfrac{275}{1}\)
Em cảm ơn chị nhiều nhiều nha!