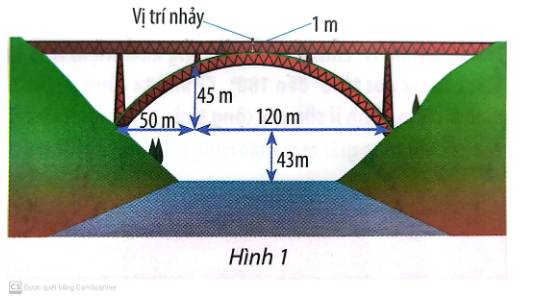
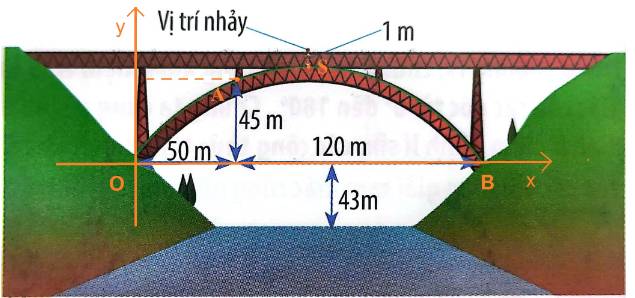
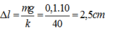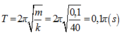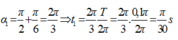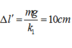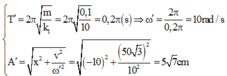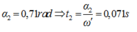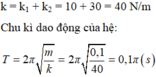Một người đàn ông có chiều cao h0 = 2 m thực hiện trò nhảy từ một nền ở chiều cao h = 25 m trên một hồ nước. Một đầu của một sợi dây đàn hồi được gắn vào chân và đầu kia cố định vào nền này. Ông này bắt đầu rơi xuống với vận tốc đầu bằng không theo phương thẳng đứng.
Chiều dài và tính đàn hồi của sợi dây được chọn sao cho tốc độ của người nhảy giảm dần bằng không khi đầu chạm mặt nước. Cuối cùng, người nhảy được treo trên dây, với đầu cách mặt mặt nước 8 m.
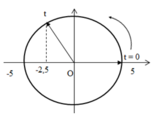
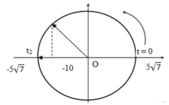
Tìm chiều dài tự nhiên của sợi dây và tốc độ tối đa và gia tốc đạt được trong thời gian nhảy.