Bài 1:Tính giá trị biểu thức:
\(1\dfrac{13}{15}.\left(0,5\right)^2.3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right):1\dfrac{23}{14}\)
Bài 2: Tính Tổng:
\(S_n=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{n\left(n+1\right)\left(n+2\right)}\)
Trình bày lời giải và đừng làm tắt bước nhé!

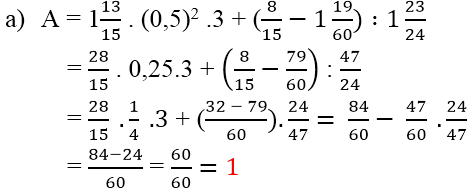
Bài 2.
\(S_n=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+...+\dfrac{1}{n\left(n+1\right)\left(n+2\right)}\)
\(\Rightarrow S_n=\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{n\left(n+1\right)}-\dfrac{1}{\left(n+1\right)\left(n+2\right)}\)\(\Rightarrow S_n=\dfrac{1}{1.2}-\dfrac{1}{\left(n+1\right)\left(n+2\right)}\)
Bài 1:
\(1\dfrac{13}{15}.\left(0,5\right)^2.3+\left(\dfrac{8}{15}-1\dfrac{19}{60}\right):1\dfrac{23}{14}\)
\(=\dfrac{28}{15}.\dfrac{1}{4}.3+\left(\dfrac{8}{15}-\dfrac{79}{60}\right):\dfrac{47}{24}\)
\(=\dfrac{28}{15}.\dfrac{1}{4}.3+\left(\dfrac{-47}{60}\right):\dfrac{47}{24}\)
\(=\dfrac{7}{15}.3+\left(\dfrac{-47}{60}\right):\dfrac{47}{24}\)
\(=\dfrac{7}{5}+\left(\dfrac{-47}{60}\right):\dfrac{47}{24}\)
\(=\dfrac{7}{5}+\dfrac{-2}{5}\)
\(=\dfrac{5}{5}=1\)